Software: CAD - Tutorial - Optimierung - Globale Suche
Die Zusammenhänge zwischen den Abmessungen der Biegefeder und den Werten der Bewertungsgrößen sind nichtlinear:
- Die berücksichtigten physikalischen Effekte enthalten Abhängigkeiten mit unterschiedlichsten Exponenten (von -3 bis +3).
- Es ist deshalb schwierig bis unmöglich, bei Berücksichtigung mehrerer Anforderungen die optimale Lösung durch analytische Berechnung oder durch "Probieren" zu finden.
Es ist immer günstig, wenn man Zusammenhänge zwischen den veränderlichen Parametern eines Systems und den sich daraus ergebenden Ergebnisgrößen grafisch veranschaulichen kann:
- Bei zwei variablen Parametern und geringem Zeitaufwand zur Ermittlung einer Stützstelle ist dafür die Raster-Suche als globales Suchverfahren der numerischen Optimierung sehr gut geeignet.
- Innerhalb vorgegebener Grenzen für jeden Parameter erfolgt eine gleichmäßige Abtastung des damit aufgespannten Suchraumes.
- Die Anzahl der möglichen Stützstellen ist abhängig von der zumutbaren Berechnungszeit (z.B. maximal einige Minuten).
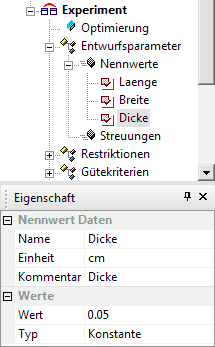
Wir vereinfachen am Anfang das Problem von drei auf zwei Optimierungsvariablen, indem wir eine konstante Dicke=0,5 mm für das Blech der Biegefeder annehmen (Typ=Konstante):
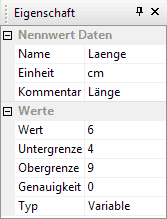
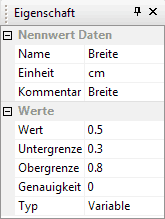
Die anderen beiden variablen Abmessungen erhalten die folgenden Grenzwerte:
- Laenge = 40 mm ... 90 mm
- Breite = 3 mm ... 8 mm
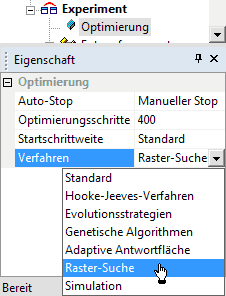
Als Optimierungsverfahren wählen wir die Raster-Suche mit 400 Schritten, was einem Raster von 20x20 Stützstellen entspricht (Empfehlung 225=15x15 für schwache PC):
Für die beiden Restriktionen tragen wir die geforderten Grenzwerte ein:
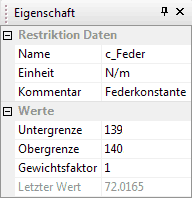
- c_Feder = (140+xx) N/m (mit xx=00..99)
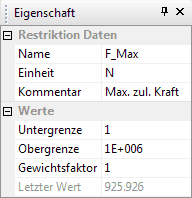
- F_Max ≥ 1 N
- Dabei wählen wir für c_Feder ein schmales, zulässiges Toleranzband (z.B. 1 N/m breit). Dieses Toleranzband ist so zu platzieren, dass die Lösung zum richtigen Grenzwert konvergiert. Da eine möglichst hohe Resonanzfrequenz gefordert wird, entspricht dies einer Tendenz zu größeren Federsteifen → also z.B. für xx=00 ergibt sich Bereich = (139..140) N/m.
- Die maximal zulässige Kraft F_Max ist nach oben praktisch unbegrenzt, was durch einen entsprechend großen Wert repräsentiert wird:
Nachdem wir das Experiment soweit konfiguriert haben, speichern wir den aktuellen Zustand. Danach starten wir die Berechnung ![]() (Projekt > Start):
(Projekt > Start):
- Im geöffneten Windows-Taskmanager können wir beobachten, wie Inventor.exe als Prozess gestartet wird.
- Dann beginnt die systematische Berechnung aller Stützstellen entsprechend der Rastersuche.
- Während die Berechnung läuft, können wir die Ergebnisse in geeigneten Diagrammen darstellen.
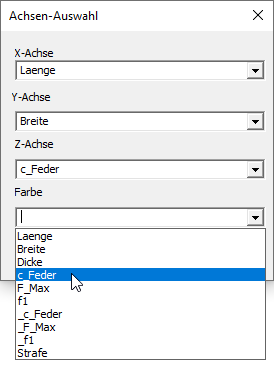
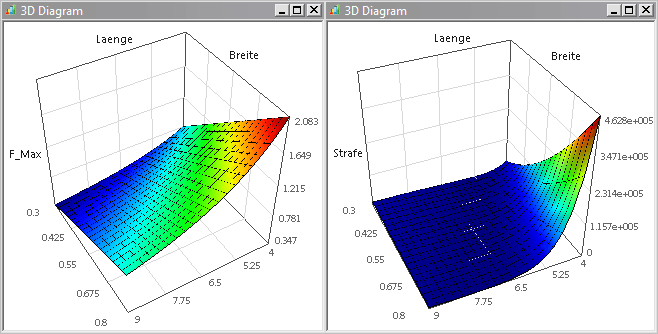
- Um einen Eindruck von der Abhängigkeit der Federkonstanten c_Feder=f(Laenge,Breite) und der Resonanzfrequenz f1=f(Laenge,Breite) zu erhalten, konfigurieren wir dafür unter Analyse > Darstellung > 3D-Darstellung entsprechende Diagramme:
- Hinweis: Mit der Version OptiY 4.7 hat sich die Form der 3D-Darstellung leicht geändert. Das Konfigurationsfenster lässt die Definition des Farbverlaufs nun unabhängig von den Achsen zu. Wir wählen im Weiteren Verlauf der Übung den Parameter für "Farbe" immer identisch zur "Z-Achse". Damit entsprechen die 3D-Darstellungen mit Ausnahme der neuen Farbgebung weiterhin dieser Anleitung. Da die Ansichtsrotation und Liniendarstellung der neuen Version noch nicht voll ausgereift sind, bleiben die folgenden Abbildungen zunächst unverändert.
- Die Funktionsflächen entstehen bereits während der Optimierung.
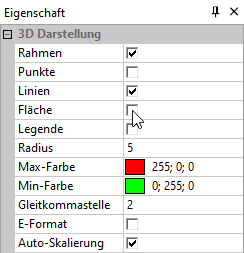
- Dazu muss man die 3D-Diagramme jedoch entsprechend konfigurieren (Diagramm mit Cursor anklicken, Eigenschaften im Experiment-Browser editieren):
- Da zusätzlich die maximal zulässige Kraft F_Max überprüft werden muss und man wissen möchte, ob überhaupt zulässige Lösungen (Strafe=0) existieren, stellen wir diese Bewertungsgrößen ebenfalls in 3D-Diagrammen dar:
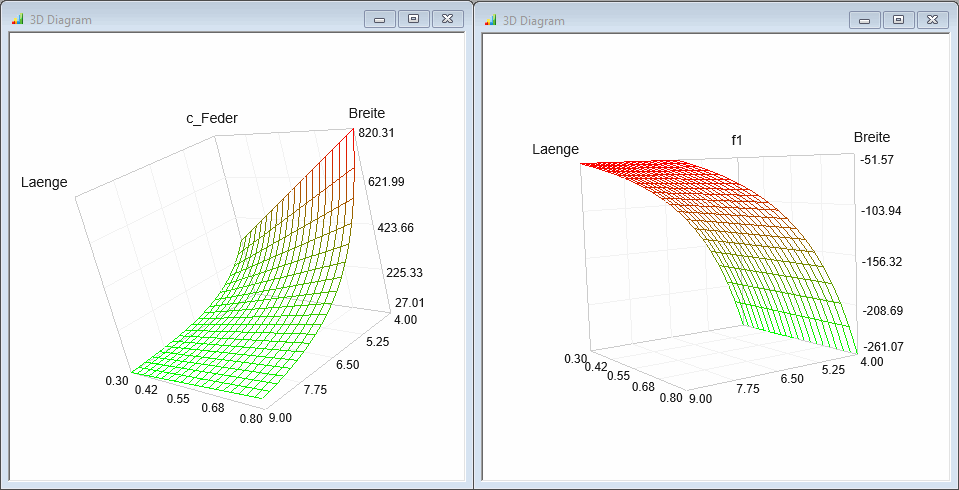
Diesen Diagrammen kann man folgende Informationen entnehmen:
- Die Federkonstante c_Feder=140 N/m lässt sich bei gegebener Federdicke durch alle Kombinationen von Länge und Breite entlang der Höhenlinie 140 N/m realisieren.
- Von diesen Kombinationen sollte man diejenige als optimale Lösung benutzen, welche die höchste Resonanzfrequenz f1 besitzt und die Belastung mit einer Kraft von 1 N verträgt.
- Die Kraft von 1 N kann kritisch werden, weil die maximal zulässige Kraft F_Max in diesem Bereich in der gleichen Größenordnung liegt.
- Das auomatisch generierte Gütekriterium Strafe widerspiegelt mit seinem Wert den quadratischen Abstand zum zulässigen Lösungsbereich.
- Im zulässigen Lösungsbereich sind keine Restriktionsgrenzen verletzt (Strafe=0).
- An der automatisch skalierten Z-Achse des Strafe-Diagramms erkennt man als untere Grenze=0. D.h., es existieren zulässige Lösungen.
- Leider erkennt man aufgrund der ungünstigen Skalierung nicht den zulässigen Bereich auf der Strafe-Funktionsfläche.
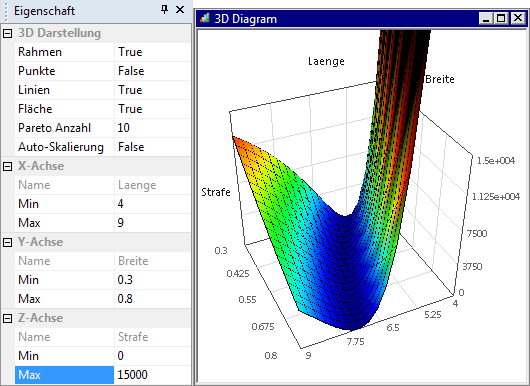
- Dies lässt sich ändern, indem man die automatische Skalierung deaktiviert und einen günstigen oberen Grenzwert für die Z-Achse angibt:
- Nun erkennt man deutlich das praktisch lineare Tal mit Strafe=0, welches der projizierten Höhenlinie c_Feder=140 N/m unter Berücksichtigung der maximal zulässigen Kraft F_Max≥1 N entspricht .
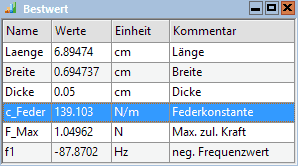
- Den Bestwert im Sinne des Frequenzkriteriums kann man ablesen unter Analyse > Bestwert > Parameter anzeigen:
Hinweis: Der angezeigte Bestwert wird nicht dem mathematisch "exakten" Optimum entsprechen, weil nur Werte der Stützstellen der Rastersuche berücksichtigt werden.
Eine Einbeziehung der Feder-Dicke als zusätzliche dritte Optimierungsvariable ist für die globale Suche nicht sinnvoll:
- Die Darstellung in 3D-Diagrammen ist unübersichtlich, da eigentlich 4D-Diagramme benötigt werden.
- Die Berechnungszeit erhöht sich mit der Potenz der Anzahl der Optimierungsvariablen. Bei gleicher Rasterdichte 20x20x20 sind bereits 8000 Stützstellen erforderlich. Damit erhöht sich die Berechnungszeit von ca. 2:30 min auf fast 1 Stunde!