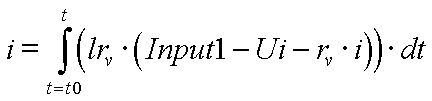Grundlagen: Simulation: Unterschied zwischen den Versionen
K →Einleitung und grundlegende Begriffe: Klammer ergänzt |
|||
| (50 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div align="center">[ | <div align="center">[https://www.ifte.de/mitarbeiter/kamusella.html '''Autor: Dr.-Ing. Alfred Kamusella''']</div> | ||
== Einleitung und grundlegende Begriffe == | == Einleitung und grundlegende Begriffe == | ||
Wie in den Grundlagen zum [[Grundlagen:_Entwurfsprozess|Entwurfsprozess]] beschrieben, werden bei der Suche optimaler Lösungen unterschiedliche Mittel und Methoden benutzt. Die verwendeten "Modelle" sind unterschiedlichster Natur, z.B.: | Wie in den Grundlagen zum [[Grundlagen:_Entwurfsprozess|Entwurfsprozess]] beschrieben, werden bei der Suche optimaler Lösungen unterschiedliche Mittel und Methoden benutzt. Die verwendeten "Modelle" sind unterschiedlichster Natur, z.B.: | ||
* [ | * [https://de.wikipedia.org/wiki/Wissen Wissen] über den Objektbereich (Basis für Gedankenexperimente) mit [https://de.wikipedia.org/wiki/Fachliteratur Fachliteratur] und [https://de.wikipedia.org/wiki/Standard Standards/Normen] als externe Wissensspeicher | ||
* [ | * [https://de.wikipedia.org/wiki/Blockschaltbild Blockschaltbilder] und [https://de.wikipedia.org/wiki/Skizze Skizzen] als externe Hilfsmittel für Gedankenexperimente | ||
* [ | * [https://de.wikipedia.org/wiki/Mathematische_Formel Dimensionierungsformeln] (Papier, Bleistift, Taschenrechner) | ||
* [ | * [https://de.wikipedia.org/wiki/Computermodell Computermodelle] ([https://de.wikipedia.org/wiki/Computer_Aided_Design CAD], [https://de.wikipedia.org/wiki/Finite-Elemente-Methode Finite Elemente Methode], [https://de.wikipedia.org/wiki/Netzwerkanalyse_(Elektrotechnik) Netzwerk-Analogien]) | ||
* Versuchsmuster im Labor (Teile, Baugruppen, Gerät - reduziert auf bestimmte Aspekte: z.B. als [ | * Versuchsmuster im Labor (Teile, Baugruppen, Gerät - reduziert auf bestimmte Aspekte: z.B. als [https://de.wikipedia.org/wiki/Prototyp_(Technik) Prototyp]). | ||
In diesem Kapitel zu den Grundlagen zur Simulation soll nun nach einer begrifflichen Klärung eine verallgemeinerte Methodik der Modellentwicklung beschrieben werden. | In diesem Kapitel zu den Grundlagen zur Simulation soll nun nach einer begrifflichen Klärung eine verallgemeinerte Methodik der Modellentwicklung beschrieben werden. | ||
<span style="background-color:Yellow">[ | <span style="background-color:Yellow">[https://de.wikipedia.org/wiki/Modell '''<u>Modell</u> ''']</span><br>ist ein Ersatzobjekt, das man zur Gewinnung von Erkenntnis über ein Originalobjekt benutzt: | ||
# Ein Modell ist immer ein Abbild von einem "Original" (d.h. von "etwas anderem"). Bei einem "Original" kann es sich auch um ein Modell handeln! | # Ein Modell ist immer ein Abbild von einem "Original" (d.h. von "etwas anderem"). Bei einem "Original" kann es sich auch um ein Modell handeln! | ||
# Ein Modell bildet nur die Eigenschaften des Originals ab, die dem Modellbenutzer wichtig erscheinen: | # Ein Modell bildet nur die Eigenschaften des Originals ab, die dem Modellbenutzer wichtig erscheinen: | ||
#* Bestimmte Eigenschaften eines Modells werden als Eigenschaften des Originals interpretiert. | #* Bestimmte Eigenschaften eines Modells werden als Eigenschaften des Originals interpretiert. | ||
#* Es gibt immer Eigenschaften eines Modells, die keinen Bezug zum Original besitzen. | #* Es gibt immer Eigenschaften eines Modells, die keinen Bezug zum Original besitzen. | ||
# Ein Modell wird [ | # Ein Modell wird [https://de.wikipedia.org/wiki/Pragmatismus pragmatisch] und zweckorientiert angewendet: | ||
#* "Minimalmodell" - mit möglichst wenig Modell hinreichend viel Erkenntnis! | #* "Minimalmodell" - mit möglichst wenig Modell hinreichend viel Erkenntnis! | ||
#* Erlaubt ist, was im Sinne des angestrebten Erkenntnisgewinns nützt. | #* Erlaubt ist, was im Sinne des angestrebten Erkenntnisgewinns nützt. | ||
<span style="background-color:Yellow">[ | <span style="background-color:Yellow">[https://de.wikipedia.org/wiki/Mathematisches_Modell '''<u>Mathematisches Modell</u> ''']</span><br>ist eine Sonderform der Modelle. Es bildet die Eigenschaften des Originals auf ein mathematisches System ab (z.B. [https://de.wikipedia.org/wiki/Lineare_Algebra Lineare Algebra], [https://de.wikipedia.org/wiki/Gew%C3%B6hnliche_Differentialgleichungen Gewöhnliche Differentialgleichungen], [https://de.wikipedia.org/wiki/Fuzzy-Logik Fuzzy-Logik]): | ||
# Die Nutzung zum Erkenntnisgewinn ist möglich, weil Eigenschaften mathematischer Systeme als Aspekte der realen Welt interpretierbar sind. | # Die Nutzung zum Erkenntnisgewinn ist möglich, weil Eigenschaften mathematischer Systeme als Aspekte der realen Welt interpretierbar sind. | ||
# Algorithmen der [ | # Algorithmen der [https://de.wikipedia.org/wiki/Computer-Algebra-System Computer-Algebra] und der [https://de.wikipedia.org/wiki/Numerische_Mathematik numerischen Mathematik] ermöglichen die Behandlung in informationsverarbeitenden Systemen (z.B. Computer). | ||
<span style="background-color:Yellow">[ | <span style="background-color:Yellow">[https://de.wikipedia.org/wiki/Experiment '''<u>Experiment</u> ''']</span><br>ist in Naturwissenschaft und Technik eine methodisch angelegte Untersuchung zur empirischen Gewinnung von Information (Wissen): | ||
* Zuvor definierte Einflussgrößen (unabhängige Variablen) werden im Experiment systematisch verändert und die dadurch hervorgerufenen Änderungen anderer Größen (abhängige Variablen) wird ermittelt. | * Zuvor definierte Einflussgrößen (unabhängige Variablen) werden im Experiment systematisch verändert und die dadurch hervorgerufenen Änderungen anderer Größen (abhängige Variablen) wird ermittelt. | ||
* Die experimentelle Situation muss in einer Form dokumentiert werden, dass die Reproduzierbarkeit der Ergebnisse durch andere Bearbeiter an andern Orten und zu anderen Zeiten gewährleistet ist. | * Die experimentelle Situation muss in einer Form dokumentiert werden, dass die Reproduzierbarkeit der Ergebnisse durch andere Bearbeiter an andern Orten und zu anderen Zeiten gewährleistet ist. | ||
| Zeile 33: | Zeile 33: | ||
* Modell-Eperimente nutzen Modelle als Ersatzobjekte zum Erkenntnisgewinn über das eigentlich zu untersuchende Original. | * Modell-Eperimente nutzen Modelle als Ersatzobjekte zum Erkenntnisgewinn über das eigentlich zu untersuchende Original. | ||
<span style="background-color:Yellow">[ | <span style="background-color:Yellow">[https://de.wikipedia.org/wiki/Simulation '''<u>Simulation</u> ''']</span><br>ist allgemein die Nutzung eines Modells. Naturwissenschaftlich-technische Simulation werden in Form von Modell-Experimenten durchgeführt, um Erkenntnisse über ein "Original" zu gewinnen: | ||
* Die Fähigkeit des "Nachdenkens" über ein zu lösendes Problem auf der Grundlage des individuellen Wissens ist das wesentliche Merkmal der Gattung Mensch. Diese Art der Simulation nennt man auch Gedankenexperiment. | * Die Fähigkeit des "Nachdenkens" über ein zu lösendes Problem auf der Grundlage des individuellen Wissens ist das wesentliche Merkmal der Gattung Mensch. Diese Art der Simulation nennt man auch Gedankenexperiment. | ||
* Bei der Nutzung von mathematischen Modellen handelt es sich meist um [ | * Bei der Nutzung von mathematischen Modellen handelt es sich meist um [https://de.wikipedia.org/wiki/Computersimulation Computersimulationen] (außer man nutzt nur "Stift und Papier"!). | ||
* Computersimulationen bieten die Basis, um Prozesse des Erkenntnisgewinns zu automatisieren. | * Computersimulationen bieten die Basis, um Prozesse des Erkenntnisgewinns zu automatisieren. | ||
| Zeile 41: | Zeile 41: | ||
* Die durch den Ingenieur nutzbaren wissenschaftlichen Verallgemeinerungen bzw. Theorien haben die Eigenart, sich jeweils nur mit ausgewählten Phänomenen der Wirklichkeit zu befassen (z.B. Technische Mechanik, Theoretische Elektrotechnik, Thermodynamik). Komplexe technische Produkte erfordern eine ganzheitliche Betrachtung unter Berücksichtigung der Wechselwirkung zwischen allen Teilsystemen. | * Die durch den Ingenieur nutzbaren wissenschaftlichen Verallgemeinerungen bzw. Theorien haben die Eigenart, sich jeweils nur mit ausgewählten Phänomenen der Wirklichkeit zu befassen (z.B. Technische Mechanik, Theoretische Elektrotechnik, Thermodynamik). Komplexe technische Produkte erfordern eine ganzheitliche Betrachtung unter Berücksichtigung der Wechselwirkung zwischen allen Teilsystemen. | ||
* Je nach Zweck des zu schaffenden ganzheitlichen Modells muss man deshalb verschiedene Phänomene einschließlich ihrer Wechselwirkung in die Modellierung einbringen (z.B. Modell eines Elektromagneten mit elektrischen, magnetischen, thermischen und geometrisch-stofflichen Phänomenen). Man spricht in der Literatur auch von der [http://publications.eas.iis.fraunhofer.de/papers/1998/013/paper.pdf Modellierung und Simulation heterogener Systeme]. | * Je nach Zweck des zu schaffenden ganzheitlichen Modells muss man deshalb verschiedene Phänomene einschließlich ihrer Wechselwirkung in die Modellierung einbringen (z.B. Modell eines Elektromagneten mit elektrischen, magnetischen, thermischen und geometrisch-stofflichen Phänomenen). Man spricht in der Literatur auch von der [http://publications.eas.iis.fraunhofer.de/papers/1998/013/paper.pdf Modellierung und Simulation heterogener Systeme]. | ||
* Als Grundlage für die erforderliche "ganzheitliche Systemsimulation" eignen sich für die mathematische Modellbildung zur Zeit insbesondere aus Rechenzeitgründen meist nur die sogenannten [ | * Als Grundlage für die erforderliche "ganzheitliche Systemsimulation" eignen sich für die mathematische Modellbildung zur Zeit insbesondere aus Rechenzeitgründen meist nur die sogenannten [https://de.wikipedia.org/wiki/Differentiell-algebraische_Gleichung Differential-algebraischen Gleichungen]. Deshalb beschränkt sich das Kapitel zur Simulation im Folgenden beispielhaft auf diese Klasse von mathematischen Modellen. Als standardisierte Modell-Beschreibungssprache hat sich dafür [https://de.wikipedia.org/wiki/Modelica Modelica] etabliert, welche die Basis unterschiedlichster Simulationssysteme zur [https://de.wikipedia.org/wiki/Physikalische_Modellierung physikalischen Modellierung] bildet. | ||
* Die durchgängige Verwendung der [ | * Die durchgängige Verwendung der [https://de.wikipedia.org/wiki/Finite-Elemente-Methode Finiten Elemente Simulation] auf Grundlage [https://de.wikipedia.org/wiki/Partielle_Differentialgleichung partieller Differentialgleichungen] scheitert heute leider häufig noch an zu langen Rechenzeiten. | ||
== Methodik der Modellentwicklung == | == Methodik der Modellentwicklung == | ||
| Zeile 64: | Zeile 63: | ||
'''<u>Funktionelle Teilsysteme</u>''' | '''<u>Funktionelle Teilsysteme</u>''' | ||
* Die [ | * Die [https://de.wikipedia.org/wiki/Komplexität Komplexität] bei der Modellierung eines Gerätes oder einer Baugruppe ist nur durch Zergliederung in "funktionelle Teilsysteme" beherrschbar. | ||
* Modelle von Teilsystemen werden im folgenden "Teilmodelle" genannt. | * Modelle von Teilsystemen werden im folgenden "Teilmodelle" genannt. | ||
* Die Abgrenzung von Teilsystemen erfolgt überwiegend nach funktionellen Aspekten: | * Die Abgrenzung von Teilsystemen erfolgt überwiegend nach funktionellen Aspekten: | ||
| Zeile 70: | Zeile 69: | ||
** Die Abgrenzung von Teilsystemen ist nicht eindeutig, aber oft identisch mit der geometrischen Abgrenzung der Funktionseinheiten. | ** Die Abgrenzung von Teilsystemen ist nicht eindeutig, aber oft identisch mit der geometrischen Abgrenzung der Funktionseinheiten. | ||
* Autonome Betreibbarkeit der funktionellen Teilsysteme sichert die voneinander unabhängige Validierung der Teilmodelle: | * Autonome Betreibbarkeit der funktionellen Teilsysteme sichert die voneinander unabhängige Validierung der Teilmodelle: | ||
** <span style="background-color:Yellow">[ | ** <span style="background-color:Yellow">[https://www.software-kompetenz.de/?19210 '''validieren''']</span> = inhaltliche Glaubwürdigkeit nachweisen (im Unterschied zu) | ||
** <span style="background-color:Yellow">[ | ** <span style="background-color:Yellow">[https://de.wikipedia.org/wiki/Verifizierung '''verifizieren''']</span> = Richtigkeit (der numerischen Implementierung) nachweisen. | ||
* Ausgangspunkt für die Abgrenzung funktioneller Teilsysteme sind die [[Grundlagen:_Entwurfsprozess#Entwickeln_von_Funktionsstrukturen|Funktionsstrukturen]], welche zu Beginn der [[Grundlagen:_Entwurfsprozess#Konzeptphase|Konzeptphase]] durch Untergliedern in Teilfunktionen aus der Gesamtfunktion entwickelt werden (z.B. Funktionsstruktur mit Energiefluss für Elektro-mechanischen Antrieb): | * Ausgangspunkt für die Abgrenzung funktioneller Teilsysteme sind die [[Grundlagen:_Entwurfsprozess#Entwickeln_von_Funktionsstrukturen|Funktionsstrukturen]], welche zu Beginn der [[Grundlagen:_Entwurfsprozess#Konzeptphase|Konzeptphase]] durch Untergliedern in Teilfunktionen aus der Gesamtfunktion entwickelt werden (z.B. Funktionsstruktur mit Energiefluss für Elektro-mechanischen Antrieb): | ||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Funktionsstruktur_elektro-magnetischer_Antriebe.gif| ]]</div> | <div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Funktionsstruktur_elektro-magnetischer_Antriebe.gif| ]]</div> | ||
| Zeile 129: | Zeile 128: | ||
:* Berücksichtigt die Phänomene unterschiedlicher (meist physikalischer) Theorien in ihrer Wechselwirkung (Mechanik, Wärme, Elektronik, ...) | :* Berücksichtigt die Phänomene unterschiedlicher (meist physikalischer) Theorien in ihrer Wechselwirkung (Mechanik, Wärme, Elektronik, ...) | ||
:* Die [http://publications.eas.iis.fraunhofer.de/papers/1998/013/paper.pdf Modellierung und Simulation heterogener Systeme] entspricht dem Bedürfnis nach ganzheitlicher Simulation technischer Systeme. | :* Die [http://publications.eas.iis.fraunhofer.de/papers/1998/013/paper.pdf Modellierung und Simulation heterogener Systeme] entspricht dem Bedürfnis nach ganzheitlicher Simulation technischer Systeme. | ||
=== Definition der Teilsystem-Schnittstellen === | === Definition der Teilsystem-Schnittstellen === | ||
| Zeile 150: | Zeile 148: | ||
'''<u>Konventionen in SimulationX</u>''' | '''<u>Konventionen in SimulationX</u>''' | ||
Das Programmsystem [ | Das Programmsystem [https://www.simulationx.de/ '''SimulationX'''] der Firma [https://www.simulationx.de/iti/esi-iti.html '''ESI ITI GmbH'''] ist eine durchgängige CAE-Lösung für das Modellieren, Simulieren und Analysieren von physikalischen Effekten. SimulationX beinhaltet z.B. vorgefertigte Modellbibliotheken für die 1D-Mechanik, 3D-Mehrkörpersysteme, Antriebstechnik, Hydraulik, Pneumatik, Thermodynamik, Elektrik, elektrische Antriebe, Magnetik und Steuerung. Bei der [https://www.simulationx.de/simulationssoftware/experten/modelica-simulation.html '''Modellbildung'''] erfolgt die Verhaltensbeschreibung mittels physikalischer und signalbasierter Elemente: | ||
* Energetisch verbundene Teilsysteme bilden dabei ein Netzwerk, dass in Analogie zur elektronischen Schaltung (=elektrisches Netzwerk) berechenbar ist: | * Energetisch verbundene Teilsysteme bilden dabei ein Netzwerk, dass in Analogie zur elektronischen Schaltung (=elektrisches Netzwerk) berechenbar ist: | ||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Teilsystem-Schnittstellen_-_simx_elektr_schaltung.gif| ]]</div> | <div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Teilsystem-Schnittstellen_-_simx_elektr_schaltung.gif| ]]</div> | ||
| Zeile 208: | Zeile 206: | ||
Die Wechselwirkung an den Teilsystem-Schnittstellen findet in der Natur augenblicklich statt ("Parallelverarbeitung"). Der Mensch definiert dafür jedoch aus Gründen der Anschaulichkeit gern kausale Abfolgen, z.B.: | Die Wechselwirkung an den Teilsystem-Schnittstellen findet in der Natur augenblicklich statt ("Parallelverarbeitung"). Der Mensch definiert dafür jedoch aus Gründen der Anschaulichkeit gern kausale Abfolgen, z.B.: | ||
<div align="center">'''''[ | <div align="center">'''''[https://de.wikipedia.org/wiki/Newtonsche_Gesetze "Kraft als Ursache der Bewegungsänderung einer trägen Masse"]'''''</div> | ||
Die umgekehrte Kausalfolge, z.B.: | Die umgekehrte Kausalfolge, z.B.: | ||
<div align="center">'''''"Bewegungsänderung einer trägen Masse als Ursache einer Kraftwirkung"'''''</div> | <div align="center">'''''"Bewegungsänderung einer trägen Masse als Ursache einer Kraftwirkung"'''''</div> | ||
| Zeile 259: | Zeile 257: | ||
Der Begriff "global" bezieht sich auf ein Gesamtmodell (Netzwerk), welches i.a. aus mehreren Elementen und ihren Verbindungen besteht. | Der Begriff "global" bezieht sich auf ein Gesamtmodell (Netzwerk), welches i.a. aus mehreren Elementen und ihren Verbindungen besteht. | ||
=== Reduktion auf idealisierte Elemente === | |||
'''<u>Arten der Idealisierung bei der Modell-Bildung</u>''' | |||
Theorien der Domänen behandeln nicht direkt die materiellen Objekte, sondern nutzen immer spezielle Idealisierungen, z.B.: | |||
# [https://de.wikipedia.org/wiki/Finite-Elemente-Methode '''Finite Elemente'''] (Feldprobleme beschrieben mit [https://de.wikipedia.org/wiki/Partielle_Differentialgleichung partiellen DGL]): | |||
#* Man spricht auch von [https://de.wikipedia.org/wiki/Übertragungssystem "Systemen mit verteilten Parametern"], weil die Eigenschaften des betrachteten Raumes als Kontinuum beschrieben werden. | |||
#* Die für die physikalischen Größen berechneten Signalwerte sind ortsabhängig, | |||
# '''Elemente mit konzentrierten Parametern''' reduzieren das Raumkontinuum jeweils eines Teilsystems auf die Signale an den Teilsystem-Schnittstellen und auf die Übertragungsfunktionen zwischen den Schnittstellen. Man unterscheidet: | |||
#* zeitkontinuierliche Elemente (z.B. analoge elektr. Bauelemente, Punktmassen, Elastizitäten - beschrieben mit [https://de.wikipedia.org/wiki/Gewöhnliche_Differentialgleichung gewöhnlichen DGL]) | |||
#* zeitdiskrete Elemente (getaktete Systeme - beschrieben z.B. mit [https://de.wikipedia.org/wiki/Petri-Netz Petri-Netzen]) | |||
'''<u>Idealisierte Elemente mit konzentrierten Parametern</u>''' | '''<u>Idealisierte Elemente mit konzentrierten Parametern</u>''' | ||
Die Elemente mit konzentrierten Parametern (Netzwerk-Elemente) haben eine besondere Bedeutung in den frühen Phasen des Konstruktionsprozesses, da sie auf Grund ihrer starken Abstraktion noch keine konkrete Geometrie benötigen. Es handelt sich hierbei um "funktionelle" Elemente. | |||
Diese Netzwerk-Elemente müssen die gleiche Funktion erfüllen wie die Raumkontinua, aus denen sie abgeleitet wurden, z.B.: | |||
{| | |||
| <u>Raumkontinuum</u>: || <u>Netzwerk-Element</u>: | |||
Die | |- | ||
| '''starrer Körper ''' || Punktmasse im Schwerpunkt (translatorisch) | |||
|- | |||
| || Trägheit um Drehachse (rotatorisch) | |||
|- | |||
| '''elastischer Körper ''' || Elastizität bzw. Nachgiebigkeit (Feder) | |||
|- | |||
| '''dämpfendes Medium ''' || Dämpfung (Dämpfer) | |||
|- | |||
| '''gleitende Flächen ''' || Reibung | |||
|- | |||
| '''elektrisches Feld ''' || elektrische Kapazität (el.-statisch) | |||
|- | |||
| || ohmscher Widerstand (el. Flussfeld) | |||
|- | |||
| '''magnetisches Feld ''' || magnetischer Leitwert (Widerstand) | |||
|- | |||
| '''usw.''' || ... | |||
|} | |||
'''<u>Beispiel: Abbildung eines E-Magneten auf ein Netzwerk-Modell</u>''' | |||
Ein Elektromagnet mit einem EI-Eisenkreis soll als Systemmodell aus Elementen mit konzentrierten Parametern modelliert werden. Dabei kann man auf Grund der Symmetrie der Magnetgeometrie eine Transformation auf einen UI-Eisenkreis vornehmen. Die beiden Außenschenkel des E-Kernes werden dazu praktisch parallel "geschalten" , was im Modell durch einen entsprechend verdoppelten Eisenquerschnitt berücksichtigt wird: | |||
<div align="center"> [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Reduktion_auf_idealisierte_Elemente_-_Beispiel_E-Magnet.gif| ]] </div> | |||
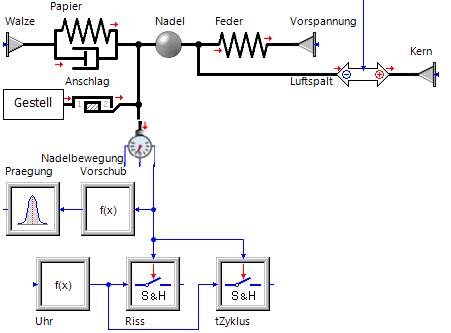
Wie man von einer konkreten Magnetgeometrie zu einer geeigneten, allgemeinen Ersatzstruktur aus Netzwerk-Elementen kommt, wird anschaulich im [[Software:_SimX_-_Nadelantrieb_-_Aktordynamik_-_Magnetkreis|Tutorial zum Prägenadel-Antrieb]] eines Blindenschriftprägers beschrieben. Deshalb wird hier nur eine Modellstruktur zu obigem Elektromagneten dargestellt: | |||
<div align="center"> [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Reduktion_auf_idealisierte_Elemente_-_Beispiel_E-Magnet-Netz.gif| ]] </div> | |||
'''<u>Die besondere Bedeutung der Zustandsgrößen</u>''' | |||
Der Zustand eines physikalischen Systems zu einem bestimmten Zeitpunkt umfasst die Gesamtheit aller seiner aktuellen physikalischen Eigenschaften. Der momentane Zustand definiert also die Werte aller ermittelbaren physikalischen Größen des betrachteten Systems. | |||
Zur eindeutigen Definition des Systemzustandes genügt ein Satz sogenannter Zustandsgrößen, wenn die Systemeigenschaften (Übertragungsfunktion und Systemparameter) bekannt sind: | |||
* Die Zustandsgrößen sind eine Teilmenge aller physikalischen Größen des Systems. | |||
* Die Werte aller anderen physikalischen Größen können aus den Werten der Zustandsgrößen berechnet werden, da durch die Systemeigenschaften die Abhängigkeiten zwischen den physikalischen Größen festgelegt sind. | |||
* Welche physikalischen Größen als Zustandsgrößen eines Systems definiert werden, ist im Prinzip willkürlich. Es muss nur gelten, dass man aus den Werten aller Zustandsgrößen die Werte aller anderen physikalischen Größen des Systems zum aktuellen Zeitpunkt berechnen kann. | |||
* Für die Modellierung dynamischer Systeme hat es sich jedoch bewährt, diejenigen Größen der Teilsystemschnittstellen als Zustandsgrößen zu definieren, welche als Ergebnis einer Integral-Berechnung sind: | |||
*# Jede dieser Zustandsgrößen repräsentiert mit ihrem aktuellem Wert die Menge von Energie, Stoff oder Information, welche sich im zugeordneten speichernden Element befindet. | |||
*# Der Wert einer Zustandsgröße ("Füllstand des Speichers") ist Resultat der vorangegangenen zeitlichen Entwicklung des Modells. | |||
*# Zum Startzeitpunkt (der zeitlichen Entwicklung) hat jede Zustandsgröße den vorzugebenden Anfangswert der Integralgröße. | |||
* Folgende Zuordnungen von Zustandsgrößen zu bestimmten Energiearten haben sich in der Modellierungspraxis für dynamische Systeme bewährt: | |||
{| | |||
| <u>Gespeicherte Energie</u>: || <u>energetische Zustandsgröße</u>: | |||
|- | |||
| '''Potentielle mechanische Energie ''' || ''Position'' einer Masse im Kraftfeld | |||
|- | |||
| '''Kinetische mechanische Energie ''' || ''Geschwindigkeit'' einer Masse | |||
|- | |||
| '''Elektr. Energie im Kondensator ''' || ''Elektrische Spannung'' am Kondensator | |||
|- | |||
| '''Magnet-Energie in einer Spule ''' || ''Elektrischer Strom'' durch die Spule | |||
|- | |||
| '''Energie des magnetischen Feldes ''' || ''Magnetischer Fluss'' im Raum | |||
|- | |||
| '''Wärmeenergie in Körper ''' || ''Temperaturdifferenz'' zur Umgebung | |||
|- | |||
| '''Pot. Energie kompressibler Medien ''' || ''Druck'' im Behälter | |||
|} | |||
'''<u>Numerische Zustandsgrößen</u>''' | |||
Auch bei der numerischen Lösung der Gleichungssysteme während der Modell-Berechnung spielen Zustandsgrößen eine Rolle: | |||
* Es handelt sich hierbei um die unabhängige Variablen des zu lösenden Gleichungssystems. Diese werden als Primär-Ergebnisse vom Solver berechnet. | |||
* Alle anderen Variablen des Modells können aus den Zustandsgrößen über mathematische Abhängigkeiten berechnet werden (Sekundär-Ergebnisse). | |||
* Die energetischen Zustandsgrößen dynamischer Systeme sind im Normalfall gleichzeitig unabhängige Variable im Sinne der Numerik. Das gilt jedoch nicht umgekehrt! | |||
* Für die Lösung eines Modell-Gleichungssystems werden zusätzliche numerische Zustandsgrößen generiert, wenn dies zur Berücksichtigung zusätzlicher Zwangsbedingungen erforderlich ist. Dies ist bei [https://de.wikipedia.org/wiki/Algebro-Differentialgleichung differential-algebraischen Gleichungen] der Fall. | |||
=== Zusammenstellung wesentlicher Effekte === | |||
<span style="background-color:Yellow">'''<u>Effekt</u> '''</span> | |||
* Gesetz (Grundzusammenhang) zur Beschreibung eines physikalischen, chemischen, biologischen, finanziellen, technischen o.ä. Geschehens. | |||
* Jedes idealisierte Element wird durch mindestens einen Effekt beschrieben. | |||
* Welche Effekte für die idealisierten Elemente des Teilmodells benötigt werden, ist abhängig vom Einsatzzweck des Modells! | |||
<span style="background-color:Yellow">'''<u>Beispiele</u>'''</span> | |||
:[https://de.wikipedia.org/wiki/Elektrischer_Widerstand '''<u>Elektrischer Widerstand:</u>'''] | |||
{| | |||
| '''ohmsches Gesetz ''' || R=u/i | |||
|- | |||
| '''Dimensionierungsgleichung ''' || R=ρ·l/A | |||
|- | |||
| '''Temperaturabhängigkeit ''' || R(T)=R<sub>20</sub>·(1+α<sub>th</sub>·ΔT) | |||
|- | |||
| '''elektrische Verlustleistung ''' || P<sub>el</sub> =u·i | |||
|- | |||
| '''usw.''' || ... | |||
|} | |||
:[https://de.wikipedia.org/wiki/Elektrische_Kapazität '''<u>Elektrischer Kapazität:</u>'''] | |||
{| | |||
| '''Kondensatorladung (C=konst.) ''' || [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Zusammenstellung_wesentl_Effekte_-_aufladung_c_konst.gif| ]] | |||
|- | |||
| '''Kondensatorladung (allgemein) ''' || [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Zusammenstellung_wesentl_Effekte_-_aufladung_allg.gif| ]] | |||
|- | |||
| '''Dimensionierungsgleichung ''' || [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Zusammenstellung_wesentl_Effekte_-_dim_gleichung_c.gif| ]] | |||
|- | |||
| '''Temperaturabhängigkeit ''' || [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Zusammenstellung_wesentl_Effekte_-_temp_abhaengigkeit.gif| ]] | |||
|- | |||
| '''gespeichert Energie (C=konst.) ''' || [[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Zusammenstellung_wesentl_Effekte_-_ladungsenergie.gif| ]] | |||
|- | |||
| '''usw.''' || ... | |||
|} | |||
=== Modell-Notation === | |||
Modell-Notation ist "nur" ein formaler Prozess der Überführung des Wissens über die Teilsysteme und ihrer Wechselwirkung in das konkrete Simulationssystem. Die kreativen Leistungen wurden in den bereits absolvierten Etappen der Teilsystem-Modellierung vollbracht: | |||
# '''Abgrenzung''' des Teilsystems; | |||
# '''Schnittstellen''' definieren (energetische Kopplungen mit kausalen und physikalischen Wirkungsrichtungen); | |||
# '''Reduktion''' auf idealisierte Elemente mit Wirkungsrichtungen der physikalischen Größen; | |||
# '''Wesentliche Effekte''' zusammenstellen. | |||
Man unterscheidet zwei grundsätzliche Formen der Modellnotation, welche in modernen Simulationssystemen gemischt angewendet werden: | |||
'''<u>1. Schaltungsorientierte Modellnotation mit grafischen Elementen</u>''' | |||
:'''A. Schaltung wie für elektronische Analogrechner''' | |||
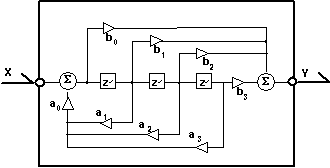
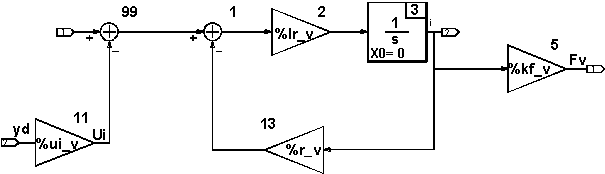
:* "Lowlevel"-Rechenschaltung aus Summatoren, Multiplikatoren, Integratoren usw. (Beispiel mit einer älteren Version des Simulationssystems von [https://www.ni.com/matrixx/ MATRIXx]): | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_analogrecher_schaltung.gif| ]]</div> | |||
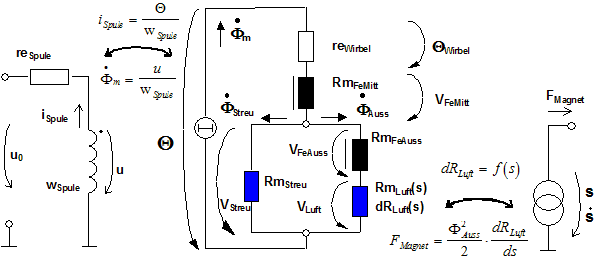
:* Das Schaltungsbeispiel enthält die Formel-Zusammenhänge für einen elektro-mechanischen Wandler (Elektromagnet): | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_magnetkraft.gif| ]]</div> | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_ind_spannung.gif| ]]</div> | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_spulenstrom.gif| ]]</div> | |||
:* Die Verbindungen zwischen den Elementen realisieren reine Signalflüsse (nicht wechselwirkend). | |||
:* Die erforderliche Wechselwirkung wird über Rückkopplungsschleifen realisiert. | |||
:'''B. Netzwerk-Analogie''' | |||
:* Diese Form der Modellnotation bewegt sich auf dem Niveau der idealisierten konzentrierten Elemente der unterschiedlichen physikalischen Domänen (Elastizität, Dämpfung, Punktmasse usw.) sowie zusätzlicher Signalglieder. | |||
:* Die Verbindungen zwischen den Signalgliedern realisieren wie bei der "Analogrechen-Schaltung" reine Signalflüsse. | |||
:* Wesentliches Merkmal der Netzwerk-Analogie sind jedoch die energetischen Verbindungen zwischen den konzentrierten Elementen. Diese bilden die direkte physikalische Wechselwirkung zwischen diesen Elementen ab: | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_netzwerk_analogie.gif| ]]</div> | |||
:'''C. Teilmodell-Blockschaltung''' | |||
:* Modelle der Teilsysteme (=Teilmodelle) enthalten komplexe Modellstrukturen meist auf Basis konzentrierter Elemente. | |||
:* Die Verbindungen zwischen den Modellen der Teilsysteme bilden die physikalische Wechselwirkung ab: | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_teilmodell_blockschaltung.gif| ]]</div> | |||
'''<u>2. Programmiersprache (Algorithmus und Equation)</u>''' | |||
* Berechnungsanweisungen in alfanumerischen Programmiersprachen weisen eine gewisse Ähnlichkeit mit der mathematischen Notation der Effekte auf (ideal wäre sicher die Eingabe mit Formel-Editor). | |||
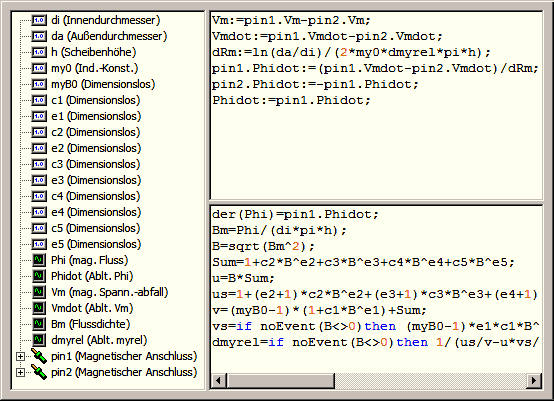
* Alle Simulationssysteme besitzen Möglichkeiten (mehr oder weniger komfortabel) mittels einer modifizierten Programmiersprache die Effekte in den Modelle zu implementieren (im Bild eine ältere Version des Typ-Designers von [https://www.simulationx.com/de/ SimulationX]): | |||
<div align="center">[[Datei:Grundlagen_Simulation_-_Methodik_der_Modellentwicklung_-_Modellnotation_programmiersprache.gif| ]]</div> | |||
* Moderne Simulationssysteme unterscheiden zwischen Algorithmen und Gleichungen: | |||
** Der Gleichungsabschnitt (im Beispiel unten) kann die zu berücksichtigenden Effekte in ungeordneter Reihenfolge enthalten. Der Solver sucht eine Lösung, die allen Gleichungen (Effekten) genügt. | |||
** Im Algorithmen-Abschnitt muss der Modellierer selbst die "Programm"-Anweisungen in der richtigen Reihenfolge anordnen. Verzweigungen und Schleifen sind möglich. | |||
== Modellberechnung == | |||
Mit dem Schwerpunkt auf idealisierte Modell-Elemente mit konzentrierten Parametern wurde in den vorherigen Abschnitten der Prozess der Modellbildung beschrieben. Nun gilt es, diese Modelle mittels numerischer Simulation zum Leben zu erwecken, um mit Hilfe von Modell-Experimenten Erkenntnisse gewinnen zu können. | |||
Das Wesen der numerischen Simulation besteht in der Berechnung der Ergebnisgrößen eines Modells aus den aktuellen Modellparametern (und Anfangswerten eventueller physikalischer Zustandsgrößen). Diese Berechnung wird in einem Simulationssystem vom sogenannten Solver vorgenommen. | |||
''' | Im Weiteren wird mit Schwerpunkt auf die Simulation dynamischer Systeme im Zeitbereich erläutert, wie solche Solver prinzipiell arbeiten und wie sie zu konfigurieren sind → [[Grundlagen:_Simulation_-_Solver|'''Kapitel: "Grundlagen Simulation (Solver)"''']] | ||
Aktuelle Version vom 23. September 2025, 10:34 Uhr
Einleitung und grundlegende Begriffe
Wie in den Grundlagen zum Entwurfsprozess beschrieben, werden bei der Suche optimaler Lösungen unterschiedliche Mittel und Methoden benutzt. Die verwendeten "Modelle" sind unterschiedlichster Natur, z.B.:
- Wissen über den Objektbereich (Basis für Gedankenexperimente) mit Fachliteratur und Standards/Normen als externe Wissensspeicher
- Blockschaltbilder und Skizzen als externe Hilfsmittel für Gedankenexperimente
- Dimensionierungsformeln (Papier, Bleistift, Taschenrechner)
- Computermodelle (CAD, Finite Elemente Methode, Netzwerk-Analogien)
- Versuchsmuster im Labor (Teile, Baugruppen, Gerät - reduziert auf bestimmte Aspekte: z.B. als Prototyp).
In diesem Kapitel zu den Grundlagen zur Simulation soll nun nach einer begrifflichen Klärung eine verallgemeinerte Methodik der Modellentwicklung beschrieben werden.
Modell
ist ein Ersatzobjekt, das man zur Gewinnung von Erkenntnis über ein Originalobjekt benutzt:
- Ein Modell ist immer ein Abbild von einem "Original" (d.h. von "etwas anderem"). Bei einem "Original" kann es sich auch um ein Modell handeln!
- Ein Modell bildet nur die Eigenschaften des Originals ab, die dem Modellbenutzer wichtig erscheinen:
- Bestimmte Eigenschaften eines Modells werden als Eigenschaften des Originals interpretiert.
- Es gibt immer Eigenschaften eines Modells, die keinen Bezug zum Original besitzen.
- Ein Modell wird pragmatisch und zweckorientiert angewendet:
- "Minimalmodell" - mit möglichst wenig Modell hinreichend viel Erkenntnis!
- Erlaubt ist, was im Sinne des angestrebten Erkenntnisgewinns nützt.
Mathematisches Modell
ist eine Sonderform der Modelle. Es bildet die Eigenschaften des Originals auf ein mathematisches System ab (z.B. Lineare Algebra, Gewöhnliche Differentialgleichungen, Fuzzy-Logik):
- Die Nutzung zum Erkenntnisgewinn ist möglich, weil Eigenschaften mathematischer Systeme als Aspekte der realen Welt interpretierbar sind.
- Algorithmen der Computer-Algebra und der numerischen Mathematik ermöglichen die Behandlung in informationsverarbeitenden Systemen (z.B. Computer).
Experiment
ist in Naturwissenschaft und Technik eine methodisch angelegte Untersuchung zur empirischen Gewinnung von Information (Wissen):
- Zuvor definierte Einflussgrößen (unabhängige Variablen) werden im Experiment systematisch verändert und die dadurch hervorgerufenen Änderungen anderer Größen (abhängige Variablen) wird ermittelt.
- Die experimentelle Situation muss in einer Form dokumentiert werden, dass die Reproduzierbarkeit der Ergebnisse durch andere Bearbeiter an andern Orten und zu anderen Zeiten gewährleistet ist.
- Experimente in der naturwissenschaftlichen Grundlagenforschung sind immer "kausal" orientiert („welche Folgen entstehen aus gegebenen Ursachen?“).
- Experimente in angewandten Wissenschaften und Technik sind meist "final" orientiert („durch welche Mittel wird ein angestrebter Zweck erreicht?“).
- Modell-Eperimente nutzen Modelle als Ersatzobjekte zum Erkenntnisgewinn über das eigentlich zu untersuchende Original.
Simulation
ist allgemein die Nutzung eines Modells. Naturwissenschaftlich-technische Simulation werden in Form von Modell-Experimenten durchgeführt, um Erkenntnisse über ein "Original" zu gewinnen:
- Die Fähigkeit des "Nachdenkens" über ein zu lösendes Problem auf der Grundlage des individuellen Wissens ist das wesentliche Merkmal der Gattung Mensch. Diese Art der Simulation nennt man auch Gedankenexperiment.
- Bei der Nutzung von mathematischen Modellen handelt es sich meist um Computersimulationen (außer man nutzt nur "Stift und Papier"!).
- Computersimulationen bieten die Basis, um Prozesse des Erkenntnisgewinns zu automatisieren.
Ganzheitliche Systemsimulation
- Die durch den Ingenieur nutzbaren wissenschaftlichen Verallgemeinerungen bzw. Theorien haben die Eigenart, sich jeweils nur mit ausgewählten Phänomenen der Wirklichkeit zu befassen (z.B. Technische Mechanik, Theoretische Elektrotechnik, Thermodynamik). Komplexe technische Produkte erfordern eine ganzheitliche Betrachtung unter Berücksichtigung der Wechselwirkung zwischen allen Teilsystemen.
- Je nach Zweck des zu schaffenden ganzheitlichen Modells muss man deshalb verschiedene Phänomene einschließlich ihrer Wechselwirkung in die Modellierung einbringen (z.B. Modell eines Elektromagneten mit elektrischen, magnetischen, thermischen und geometrisch-stofflichen Phänomenen). Man spricht in der Literatur auch von der Modellierung und Simulation heterogener Systeme.
- Als Grundlage für die erforderliche "ganzheitliche Systemsimulation" eignen sich für die mathematische Modellbildung zur Zeit insbesondere aus Rechenzeitgründen meist nur die sogenannten Differential-algebraischen Gleichungen. Deshalb beschränkt sich das Kapitel zur Simulation im Folgenden beispielhaft auf diese Klasse von mathematischen Modellen. Als standardisierte Modell-Beschreibungssprache hat sich dafür Modelica etabliert, welche die Basis unterschiedlichster Simulationssysteme zur physikalischen Modellierung bildet.
- Die durchgängige Verwendung der Finiten Elemente Simulation auf Grundlage partieller Differentialgleichungen scheitert heute leider häufig noch an zu langen Rechenzeiten.
Methodik der Modellentwicklung
Nur eine "gewisse" Systematik bei der Entwicklung numerischer Modelle führt mit vertretbarem Aufwand zu qualitativ hochwertigen Modellen, welche für den angestrebten Zweck nutzbar sind:
- Die nachfolgenden Schritte haben sich bei der Entwicklung von Modellen mit konzentrierten Parametern (Netzwerkanalogien) bewährt:
- Teilsysteme abgrenzen
- Schnittstellen der Teilsysteme definieren
- Reduktion auf idealisierte Elemente
- Wesentliche Effekte zusammenstellen
- Modell-Notation (Teilmodelle / gesamte Modellstruktur)
- Im Prinzip ist diese Schrittfolge aber auch für andere Modellklassen anwendbar (z.B. Finite Elemente Modelle, geometrisch-stoffliche Modellbaukästen).
Die einzelnen Schritte der Modellbildung werden im Folgenden näher erläutert.
Abgrenzung von Teilsystemen
Funktionelle Teilsysteme
- Die Komplexität bei der Modellierung eines Gerätes oder einer Baugruppe ist nur durch Zergliederung in "funktionelle Teilsysteme" beherrschbar.
- Modelle von Teilsystemen werden im folgenden "Teilmodelle" genannt.
- Die Abgrenzung von Teilsystemen erfolgt überwiegend nach funktionellen Aspekten:
- Es sollten funktionelle Einheiten entstehen, welche sowohl als reale Objekte als auch als Teilmodelle selbstständig betrieben werden können.
- Die Abgrenzung von Teilsystemen ist nicht eindeutig, aber oft identisch mit der geometrischen Abgrenzung der Funktionseinheiten.
- Autonome Betreibbarkeit der funktionellen Teilsysteme sichert die voneinander unabhängige Validierung der Teilmodelle:
- validieren = inhaltliche Glaubwürdigkeit nachweisen (im Unterschied zu)
- verifizieren = Richtigkeit (der numerischen Implementierung) nachweisen.
- Ausgangspunkt für die Abgrenzung funktioneller Teilsysteme sind die Funktionsstrukturen, welche zu Beginn der Konzeptphase durch Untergliedern in Teilfunktionen aus der Gesamtfunktion entwickelt werden (z.B. Funktionsstruktur mit Energiefluss für Elektro-mechanischen Antrieb):
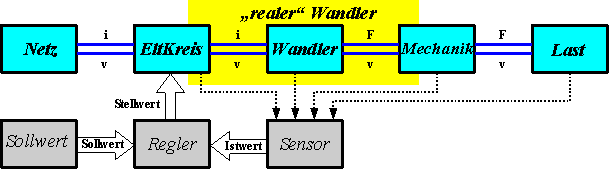
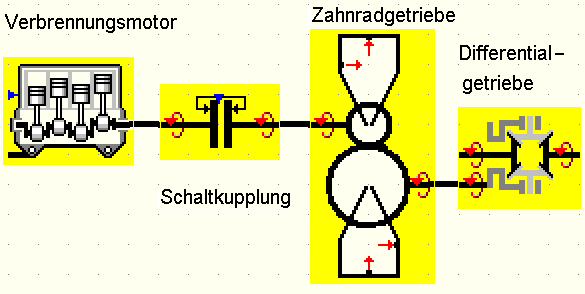
- Funktionelle Teilsysteme eines elektromagnetischen Antriebssystems sind dann z.B. Netzteil, elektronische Ansteuerung, elektromagnetischer Wandler, Getriebemechanik und Lastsystem:
- Der Energiefluss zwischen den Teilsystemen wird im Beispiel durch elektrische Größen (Spannung v und Strom i) sowie mechanische Größen (Geschwindigkeit v und Kraft F) repräsentiert.
Basis-Modellstruktur und Basis-Teilmodelle
Für typische Entwurfsaufgaben lassen sich verallgemeinerte Funktionsstrukturen definieren. Beim Vorliegen einer konkreten Entwurfsaufgabe kann man dann ausgehend von diesen verallgemeinerten Strukturen die erforderlichen Teilfunktionen abgrenzen:
- Basis-Modellstruktur (z.B. einer Geräteklasse):
- Verallgemeinerte Zerlegung in Teilsysteme
- Verallgemeinerter Energie-, Stoff- und Informationsfluss (Funktionsstruktur)
- Basis-Teilmodelle:
- Abstrakte Teilmodelle zu den Teilsystemen einer Basis-Modellstruktur.
- "ohne Inhalt" - nur funktionelle Abgrenzung und Schnittstellen (Teilfunktion)
Beispiel:
- Beim Entwurf elektromechanischer Antriebe (als Beispiel für eine "typische Entwurfsaufgabe"), kann man meist von folgender Basis-Modellstruktur ausgehen:
- Es sind folgende Basis-Teilmodelle enthalten:
- elektrische Energieversorgung (Netz)
- Ansteuerschaltung + elektrische Aspekte des elektromechanischen Wandlers (EltKreis)
- elektromechanischer Wandler ("idealisierter" Wandler)
- mechanische Aspekte des Wandlers + Übertragungsglieder zur Last (Mechanik)
- mechanische Wirkstelle (Last)
- Messglied mit Informationsverarbeitung (Sensor)
- Reglerbaugruppe (Regler)
- Sollwertvorgaben für die Bewegung (Sollwert)
- Für den "einfachen" ungeregelten Antrieb reduziert sich z.B. die erforderliche Modellstruktur um die informationsverarbeitenden Komponenten des Regelsystems.
Physikalische Domänen
- Physikalische Domäne (kurz "Domäne"):
- Stellt in einer Modellierungsumgebung (z.B. SimulationX) für jeweils eine Theorie die erforderlichen Modellbausteine bereit (Elemente und Verbindungen).
- Jede diese Theorien wird repräsentiert durch Speicher- und Übertragungselemente für eine bestimmte Energie-Art (bzw. für Stoff oder Information), z.B. in der Elektronik :
- Speicher: elektrische Kapazität und Induktivität
- Übertragungselemente: ohmscher Widerstand, ideale Diode, Schalter
- Ganzheitliche Simulation auf Basis differential-algebraischer Gleichungen:
- Nutzung einer Theorie "Verallgemeinerter Netzwerke" mit Mehrpol-Elementen.
- "Gleiche" Behandlung der unterschiedlichen Domänen durch Ausnutzung der Analogiebeziehungen zu elektrischen Netzwerken.
- Wandlerelemente:
- Realisieren die (wechselwirkende) Kopplung zwischen jeweils zwei unterschiedlichen Domänen z.B.:
- elektro-magnetischer Wandler;
- magneto-mechanischer Wandler;
- elektro-mechanischer Wandler (bei Kapselung des vermittelnden Partialsystems);
- stofflich/energetisch-ökonomischer Wandler ("Gebührenzähler")
- Genutzt werden hier die Analogiebeziehungen zum elektrischen Transformator
- Realisieren die (wechselwirkende) Kopplung zwischen jeweils zwei unterschiedlichen Domänen z.B.:
- Heterogenes Modell:
- Berücksichtigt die Phänomene unterschiedlicher (meist physikalischer) Theorien in ihrer Wechselwirkung (Mechanik, Wärme, Elektronik, ...)
- Die Modellierung und Simulation heterogener Systeme entspricht dem Bedürfnis nach ganzheitlicher Simulation technischer Systeme.
Definition der Teilsystem-Schnittstellen
Wechselwirkung
Nach der Abgrenzung eines Teilsystems muss analysiert werden, wie es mit seiner Umgebung in Kontakt tritt (stofflich, energetisch, informationell):
- Im Sinne der Netzwerk-Theorie ist ein Teilsystem ein Netzwerk-Element.
- Die Kontaktstellen werden als Pole dieses Netzwerk-Elements idealisiert.
Man unterscheidet zwei Arten des Kopplung zwischen Teilsystemen:
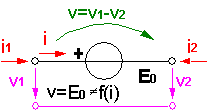
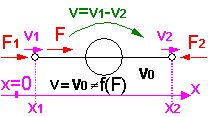
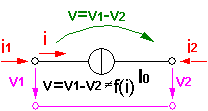
- Wechselwirkungsfrei (rückwirkungsfreie INPUT und OUTPUT), z.B. idealer Spannungsverstärker:
- Wechselwirkend (mit Rückwirkung über die Verbindungen)
- Reale technische Teilsysteme sind selten von ihrer Umgebung energetisch entkoppelt.
- Es findet meist Energieübertragung statt und diese ist nie rückwirkungsfrei, z.B. elektro-magnetischer Antrieb:
Konventionen in SimulationX
Das Programmsystem SimulationX der Firma ESI ITI GmbH ist eine durchgängige CAE-Lösung für das Modellieren, Simulieren und Analysieren von physikalischen Effekten. SimulationX beinhaltet z.B. vorgefertigte Modellbibliotheken für die 1D-Mechanik, 3D-Mehrkörpersysteme, Antriebstechnik, Hydraulik, Pneumatik, Thermodynamik, Elektrik, elektrische Antriebe, Magnetik und Steuerung. Bei der Modellbildung erfolgt die Verhaltensbeschreibung mittels physikalischer und signalbasierter Elemente:
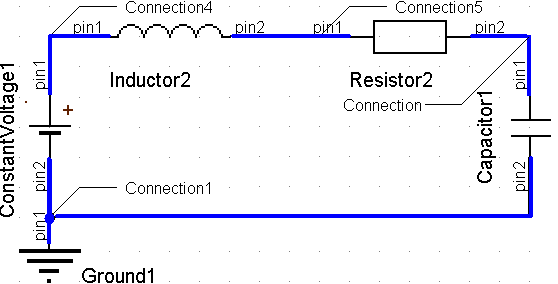
- Energetisch verbundene Teilsysteme bilden dabei ein Netzwerk, dass in Analogie zur elektronischen Schaltung (=elektrisches Netzwerk) berechenbar ist:
- So werden z.B. die idealisierten konzentrierten Elemente der Mechanik unter Beachtung der positiven Richtung der Weg-Koordinate zu einer "mechanischen Schaltung" verbunden:
- In SimulationX werden energieübertragende Schnittstellen der Teilsysteme als Anschlüsse bezeichnet (=Connector bzw. Ctr=Pin).
- Je nach Art der übertragenen Energie unterscheidet man mechanische, elektrische, hydraulische Anschlüsse (usw.).
- Nicht so deutlich wird bei SimulationX der spezielle Verbindungstyp (=Connection) zwischen 2 Anschlüssen. Für jede Energieart werden automatisch entsprechend definierte Verbindungen benutzt (mechanisch translatorisch, elektrisch, hydraulisch usw.).
Leistung=Flussgröße x Potentialgröße
Die Energieübertragung zwischen den Teilsystemen findet über die Verbindungen als kontinuierlicher Vorgang im Zeitbereich statt. Kennzeichnend dafür ist der jeweilige Momentanwert der Leistung P=dW/dt:
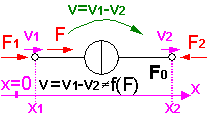
- Betrachtet man elektrische Netzwerke, so kann man an dem als Verbindung dienenden "Draht" ein Spannungspotential v in Bezug auf den Massepunkt der Schaltung messen. Durch den Draht fließt ein Strom i. Die aktuell übertragene elektrische Leistung ist Pe=v·i.
- Die mechanische Leistung Pm=v·F ist das Produkt aus Geschwindigkeit v und Kraft F, die hier als Potential- und Flussgröße des starren, mechanischen Verbindungselements benutzt werden.
- Verallgemeinerung für beliebige energetische Netzwerke:
- eine energetische Verbindung besitzt eine Potential- und eine Flussgröße;
- aktuell über die Verbindung übertragene Leistung = Flussgröße x Potentialgröße.
Analogien zwischen den Domänen
Für jede physikalische Domäne kann man theoretisch die Potential- und Flussgrößen an den Verbindungen so wählen, dass ihr Produkt der aktuell übertragenen Leistung entspricht:
Domäne | Leistung=Fluss·Potential | Potentialgröße | Flussgröße ---------------------------------------------------------------------------------------------- elektrisch | Pel = i · v | el. Spannung v | el. Strom i mech. translatorisch | Pmech = F · v | Geschwindigkeit v | Kraft F mech. rotatorisch | Prot = M · ω | Winkelgeschw. ω | Moment M akustisch | Ps = p · Q | Schalldruck p | Schallfluss Q
In der Praxis weicht man jedoch bei einigen physikalischen Domänen von diesem Prinzip ab:
Domäne | Leistung=Fluss·Potential | Potentialgröße | Flussgröße ---------------------------------------------------------------------------------------------- magnetisch | Pmagn = dΦ/dt · Vm | magn. Spannung Vm | Flussänderung . | | |(genutzt Fluss Φ wegen . | | | Analogie zum el. R) ---------------------------------------------------------------------------------------------- fluidisch | Pfl = dV/dt · p | Druck p | Volumenstrom Q . | | |(genutzt Massestrom dm/dt . | | | wegen Kompression!) ---------------------------------------------------------------------------------------------- thermisch | Pth ist bereits Leistung!| Temperatur ΔT | Wärmestrom Pth=dQ/dt . | | |(Q=Wärmemenge)
Abweichungen bei der Wahl der Analogiegrößen resultieren aus zwei wesentlichen Ursachen:
- Historisch bedingt:
- So führte man z.B. den Begriff des magnetischen Widerstandes ein, dessen Wert als Quotient aus magnetischer Spannung und magnetischem Fluss berechnet wurde.
- Diese "falsche" Analogie eines magnetischen Energiespeichers (z.B. Eisenvolumen) zum elektrischen Widerstand, welcher ein elektrisches Verlustelement darstellt, ermöglicht trotzdem richtige Berechnungen von Magnetkreisen.
- Aufgrund der "Anschaulichkeit" behielt man solche historischen Analogiebeziehungen bei. Dies gilt auch für die thermische Domäne.
- Praktikabilität:
- Bei kompressiblen Medien ist das Volumen einer bestimmten Stoffmenge abhängig vom aktuellen Druck.
- Mit dem Volumenstrom als Flussgröße kann man nur sehr umständlich die transportierte Stoffmenge berechnen.
- Deshalb nutzt man den Massestrom, aus dem man bei Bedarf relativ einfach die aktuelle Durchflussleistung berechnen kann, weil der Druck an dieser Stelle bekannt ist.
Wechselwirkung von Teilsystemen
Die Wechselwirkung an den Teilsystem-Schnittstellen findet in der Natur augenblicklich statt ("Parallelverarbeitung"). Der Mensch definiert dafür jedoch aus Gründen der Anschaulichkeit gern kausale Abfolgen, z.B.:
Die umgekehrte Kausalfolge, z.B.:
wäre zwar gewöhnungsbedürftig, aber genauso brauchbar:
- Dies widerspiegelt sich vereinfacht in der Gleichung F=m·a, die beliebig umgestellt werden kann, ohne an Gültigkeit zu verlieren.
- Moderne Simulationssysteme bilden diese Gleichzeitigkeit durch die Generierung und Lösung eines ganzheitlichen Gleichungssystems ab.
- Im Sinne der Anschaulichkeit ist es günstig, bei der Modellbildung die Datenflüsse an den Teilsystem-Schnittstellen als kausale Wirkungsrichtungen zu interpretieren:
- Grundlage für die datenfluss-orientierte Modellbildung sind folgende Annahmen:
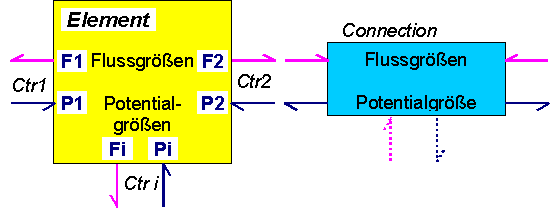
- Die Wechselwirkung zwischen den Teilsystemen (Elemente) wird über die Verbindungen (Connection) vermittelt.
- Für jede physikalische Domäne wird ein Connection-Typ definiert (z.B. elektrischer Anschluss).
- Für jeden Connection-Typ wird eine physikalische Größe als Flussgröße F (z.B. i=el.Strom) definiert.
- In der Connection gilt immer ∑Fi=0, wobei die Werte der Fi von den verbundenen Elementen in die Connection eingespeist werden.
- Für jeden Connection-Typ wird eine Potentialgröße P definiert, deren Wert jedem verbundenen Element zur Verfügung gestellt wird.
Konventionen in der Netzwerktheorie
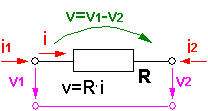
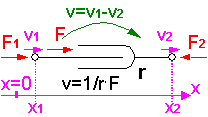
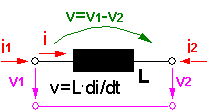
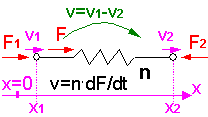
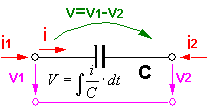
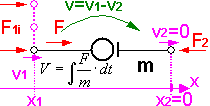
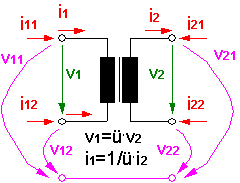
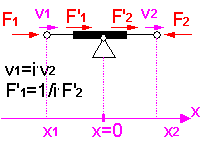
Für elektro-analoge Netzwerke gelten Konventionen für die Richtung der physikalischen Größen an den Schnittstellen und für die Bildung der Potential-Differenzen über den Netzwerk-Elementen. Dies soll an einer Gegenüberstellung äquivalenter Elemente der elektrischen und der mechanisch-translatorischen Domäne gezeigt werden:
Da auf Basis der Teilsysteme ein Baustein-System für Modelle angestrebt wird, müssen bei der Festlegung der positiven Richtungen an den Schnittstellen bestimmte Konventionen eingehalten werden:
- Im Sinne einer einfachen Übertragung von Modellen zwischen unterschiedlichen Simulationssystemen sollten dabei die Vereinbarungen der Netzwerk-Theorie genutzt werden.
- Die Festlegung der positiven Richtungen im Innern der Teilsysteme ist für die Koppelfähigkeit ohne Bedeutung. Bei Bewegungsgrößen der Mechanik sollte man z.B. im Sinne der Einheitlichkeit für die Richtung die gleichen Konventionen nutzen, wie an den Schnittstellen.
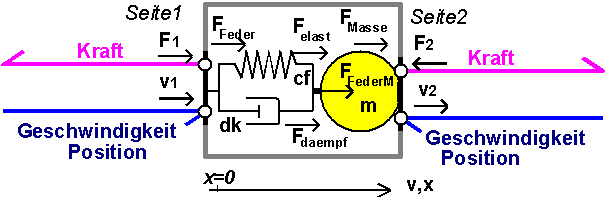
- Das folgende Bild zeigt für ein Feder-Masse-Dämpfer-Element die Datenflüsse (Halbpfeile) und die positiven physikalischen Wirkungsrichtungen ("normale" Pfeile) der berücksichtigten mechanischen Größen:
Positive Werte physikalischer Größen an Element-Schnittstellen sind wie folgt definiert:
- z.B. mechanisch-translatorischen Größen
- Kraft: in das Element hinein
- Geschwindigkeit: in positiver Wegrichtung (pos. v-Tensor an 2-Pol entspricht Elementverkürzung)
- Wegkoordinate: in Richtung einer Koordinatenachse X, Y oder Z (im globalen Koordinatensystem)
- z.B. elektrische Größen:
- elektr. Strom: in das Element hinein
- elektr. Spannung: vom Schnittstellen-Potential zum globalen Nullpotential
- verallgemeinert für "nichtmechanische" Größen:
- Flussgröße: in das Element hinein
- Potentialgröße: gegen globales Bezugspotential
Der Begriff "global" bezieht sich auf ein Gesamtmodell (Netzwerk), welches i.a. aus mehreren Elementen und ihren Verbindungen besteht.
Reduktion auf idealisierte Elemente
Arten der Idealisierung bei der Modell-Bildung
Theorien der Domänen behandeln nicht direkt die materiellen Objekte, sondern nutzen immer spezielle Idealisierungen, z.B.:
- Finite Elemente (Feldprobleme beschrieben mit partiellen DGL):
- Man spricht auch von "Systemen mit verteilten Parametern", weil die Eigenschaften des betrachteten Raumes als Kontinuum beschrieben werden.
- Die für die physikalischen Größen berechneten Signalwerte sind ortsabhängig,
- Elemente mit konzentrierten Parametern reduzieren das Raumkontinuum jeweils eines Teilsystems auf die Signale an den Teilsystem-Schnittstellen und auf die Übertragungsfunktionen zwischen den Schnittstellen. Man unterscheidet:
- zeitkontinuierliche Elemente (z.B. analoge elektr. Bauelemente, Punktmassen, Elastizitäten - beschrieben mit gewöhnlichen DGL)
- zeitdiskrete Elemente (getaktete Systeme - beschrieben z.B. mit Petri-Netzen)
Idealisierte Elemente mit konzentrierten Parametern
Die Elemente mit konzentrierten Parametern (Netzwerk-Elemente) haben eine besondere Bedeutung in den frühen Phasen des Konstruktionsprozesses, da sie auf Grund ihrer starken Abstraktion noch keine konkrete Geometrie benötigen. Es handelt sich hierbei um "funktionelle" Elemente.
Diese Netzwerk-Elemente müssen die gleiche Funktion erfüllen wie die Raumkontinua, aus denen sie abgeleitet wurden, z.B.:
| Raumkontinuum: | Netzwerk-Element: |
| starrer Körper | Punktmasse im Schwerpunkt (translatorisch) |
| Trägheit um Drehachse (rotatorisch) | |
| elastischer Körper | Elastizität bzw. Nachgiebigkeit (Feder) |
| dämpfendes Medium | Dämpfung (Dämpfer) |
| gleitende Flächen | Reibung |
| elektrisches Feld | elektrische Kapazität (el.-statisch) |
| ohmscher Widerstand (el. Flussfeld) | |
| magnetisches Feld | magnetischer Leitwert (Widerstand) |
| usw. | ... |
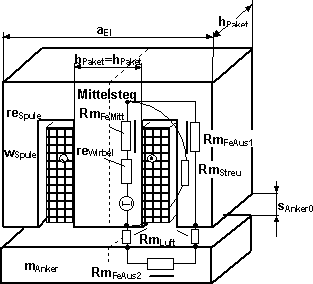
Beispiel: Abbildung eines E-Magneten auf ein Netzwerk-Modell
Ein Elektromagnet mit einem EI-Eisenkreis soll als Systemmodell aus Elementen mit konzentrierten Parametern modelliert werden. Dabei kann man auf Grund der Symmetrie der Magnetgeometrie eine Transformation auf einen UI-Eisenkreis vornehmen. Die beiden Außenschenkel des E-Kernes werden dazu praktisch parallel "geschalten" , was im Modell durch einen entsprechend verdoppelten Eisenquerschnitt berücksichtigt wird:
Wie man von einer konkreten Magnetgeometrie zu einer geeigneten, allgemeinen Ersatzstruktur aus Netzwerk-Elementen kommt, wird anschaulich im Tutorial zum Prägenadel-Antrieb eines Blindenschriftprägers beschrieben. Deshalb wird hier nur eine Modellstruktur zu obigem Elektromagneten dargestellt:
Die besondere Bedeutung der Zustandsgrößen
Der Zustand eines physikalischen Systems zu einem bestimmten Zeitpunkt umfasst die Gesamtheit aller seiner aktuellen physikalischen Eigenschaften. Der momentane Zustand definiert also die Werte aller ermittelbaren physikalischen Größen des betrachteten Systems.
Zur eindeutigen Definition des Systemzustandes genügt ein Satz sogenannter Zustandsgrößen, wenn die Systemeigenschaften (Übertragungsfunktion und Systemparameter) bekannt sind:
- Die Zustandsgrößen sind eine Teilmenge aller physikalischen Größen des Systems.
- Die Werte aller anderen physikalischen Größen können aus den Werten der Zustandsgrößen berechnet werden, da durch die Systemeigenschaften die Abhängigkeiten zwischen den physikalischen Größen festgelegt sind.
- Welche physikalischen Größen als Zustandsgrößen eines Systems definiert werden, ist im Prinzip willkürlich. Es muss nur gelten, dass man aus den Werten aller Zustandsgrößen die Werte aller anderen physikalischen Größen des Systems zum aktuellen Zeitpunkt berechnen kann.
- Für die Modellierung dynamischer Systeme hat es sich jedoch bewährt, diejenigen Größen der Teilsystemschnittstellen als Zustandsgrößen zu definieren, welche als Ergebnis einer Integral-Berechnung sind:
- Jede dieser Zustandsgrößen repräsentiert mit ihrem aktuellem Wert die Menge von Energie, Stoff oder Information, welche sich im zugeordneten speichernden Element befindet.
- Der Wert einer Zustandsgröße ("Füllstand des Speichers") ist Resultat der vorangegangenen zeitlichen Entwicklung des Modells.
- Zum Startzeitpunkt (der zeitlichen Entwicklung) hat jede Zustandsgröße den vorzugebenden Anfangswert der Integralgröße.
- Folgende Zuordnungen von Zustandsgrößen zu bestimmten Energiearten haben sich in der Modellierungspraxis für dynamische Systeme bewährt:
| Gespeicherte Energie: | energetische Zustandsgröße: |
| Potentielle mechanische Energie | Position einer Masse im Kraftfeld |
| Kinetische mechanische Energie | Geschwindigkeit einer Masse |
| Elektr. Energie im Kondensator | Elektrische Spannung am Kondensator |
| Magnet-Energie in einer Spule | Elektrischer Strom durch die Spule |
| Energie des magnetischen Feldes | Magnetischer Fluss im Raum |
| Wärmeenergie in Körper | Temperaturdifferenz zur Umgebung |
| Pot. Energie kompressibler Medien | Druck im Behälter |
Numerische Zustandsgrößen
Auch bei der numerischen Lösung der Gleichungssysteme während der Modell-Berechnung spielen Zustandsgrößen eine Rolle:
- Es handelt sich hierbei um die unabhängige Variablen des zu lösenden Gleichungssystems. Diese werden als Primär-Ergebnisse vom Solver berechnet.
- Alle anderen Variablen des Modells können aus den Zustandsgrößen über mathematische Abhängigkeiten berechnet werden (Sekundär-Ergebnisse).
- Die energetischen Zustandsgrößen dynamischer Systeme sind im Normalfall gleichzeitig unabhängige Variable im Sinne der Numerik. Das gilt jedoch nicht umgekehrt!
- Für die Lösung eines Modell-Gleichungssystems werden zusätzliche numerische Zustandsgrößen generiert, wenn dies zur Berücksichtigung zusätzlicher Zwangsbedingungen erforderlich ist. Dies ist bei differential-algebraischen Gleichungen der Fall.
Zusammenstellung wesentlicher Effekte
Effekt
- Gesetz (Grundzusammenhang) zur Beschreibung eines physikalischen, chemischen, biologischen, finanziellen, technischen o.ä. Geschehens.
- Jedes idealisierte Element wird durch mindestens einen Effekt beschrieben.
- Welche Effekte für die idealisierten Elemente des Teilmodells benötigt werden, ist abhängig vom Einsatzzweck des Modells!
Beispiele
| ohmsches Gesetz | R=u/i |
| Dimensionierungsgleichung | R=ρ·l/A |
| Temperaturabhängigkeit | R(T)=R20·(1+αth·ΔT) |
| elektrische Verlustleistung | Pel =u·i |
| usw. | ... |
| Kondensatorladung (C=konst.) | 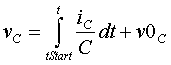
|
| Kondensatorladung (allgemein) | 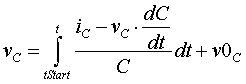
|
| Dimensionierungsgleichung | 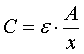
|
| Temperaturabhängigkeit | |
| gespeichert Energie (C=konst.) | 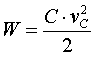
|
| usw. | ... |
Modell-Notation
Modell-Notation ist "nur" ein formaler Prozess der Überführung des Wissens über die Teilsysteme und ihrer Wechselwirkung in das konkrete Simulationssystem. Die kreativen Leistungen wurden in den bereits absolvierten Etappen der Teilsystem-Modellierung vollbracht:
- Abgrenzung des Teilsystems;
- Schnittstellen definieren (energetische Kopplungen mit kausalen und physikalischen Wirkungsrichtungen);
- Reduktion auf idealisierte Elemente mit Wirkungsrichtungen der physikalischen Größen;
- Wesentliche Effekte zusammenstellen.
Man unterscheidet zwei grundsätzliche Formen der Modellnotation, welche in modernen Simulationssystemen gemischt angewendet werden:
1. Schaltungsorientierte Modellnotation mit grafischen Elementen
- A. Schaltung wie für elektronische Analogrechner
- "Lowlevel"-Rechenschaltung aus Summatoren, Multiplikatoren, Integratoren usw. (Beispiel mit einer älteren Version des Simulationssystems von MATRIXx):
- Das Schaltungsbeispiel enthält die Formel-Zusammenhänge für einen elektro-mechanischen Wandler (Elektromagnet):
- Die Verbindungen zwischen den Elementen realisieren reine Signalflüsse (nicht wechselwirkend).
- Die erforderliche Wechselwirkung wird über Rückkopplungsschleifen realisiert.
- B. Netzwerk-Analogie
- Diese Form der Modellnotation bewegt sich auf dem Niveau der idealisierten konzentrierten Elemente der unterschiedlichen physikalischen Domänen (Elastizität, Dämpfung, Punktmasse usw.) sowie zusätzlicher Signalglieder.
- Die Verbindungen zwischen den Signalgliedern realisieren wie bei der "Analogrechen-Schaltung" reine Signalflüsse.
- Wesentliches Merkmal der Netzwerk-Analogie sind jedoch die energetischen Verbindungen zwischen den konzentrierten Elementen. Diese bilden die direkte physikalische Wechselwirkung zwischen diesen Elementen ab:
- C. Teilmodell-Blockschaltung
- Modelle der Teilsysteme (=Teilmodelle) enthalten komplexe Modellstrukturen meist auf Basis konzentrierter Elemente.
- Die Verbindungen zwischen den Modellen der Teilsysteme bilden die physikalische Wechselwirkung ab:
2. Programmiersprache (Algorithmus und Equation)
- Berechnungsanweisungen in alfanumerischen Programmiersprachen weisen eine gewisse Ähnlichkeit mit der mathematischen Notation der Effekte auf (ideal wäre sicher die Eingabe mit Formel-Editor).
- Alle Simulationssysteme besitzen Möglichkeiten (mehr oder weniger komfortabel) mittels einer modifizierten Programmiersprache die Effekte in den Modelle zu implementieren (im Bild eine ältere Version des Typ-Designers von SimulationX):
- Moderne Simulationssysteme unterscheiden zwischen Algorithmen und Gleichungen:
- Der Gleichungsabschnitt (im Beispiel unten) kann die zu berücksichtigenden Effekte in ungeordneter Reihenfolge enthalten. Der Solver sucht eine Lösung, die allen Gleichungen (Effekten) genügt.
- Im Algorithmen-Abschnitt muss der Modellierer selbst die "Programm"-Anweisungen in der richtigen Reihenfolge anordnen. Verzweigungen und Schleifen sind möglich.
Modellberechnung
Mit dem Schwerpunkt auf idealisierte Modell-Elemente mit konzentrierten Parametern wurde in den vorherigen Abschnitten der Prozess der Modellbildung beschrieben. Nun gilt es, diese Modelle mittels numerischer Simulation zum Leben zu erwecken, um mit Hilfe von Modell-Experimenten Erkenntnisse gewinnen zu können.
Das Wesen der numerischen Simulation besteht in der Berechnung der Ergebnisgrößen eines Modells aus den aktuellen Modellparametern (und Anfangswerten eventueller physikalischer Zustandsgrößen). Diese Berechnung wird in einem Simulationssystem vom sogenannten Solver vorgenommen.
Im Weiteren wird mit Schwerpunkt auf die Simulation dynamischer Systeme im Zeitbereich erläutert, wie solche Solver prinzipiell arbeiten und wie sie zu konfigurieren sind → Kapitel: "Grundlagen Simulation (Solver)"