Grundlagen: Optimierung: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
*# Man verfügt nur über begrenzte Ressourcen an Zeit und Geld. | *# Man verfügt nur über begrenzte Ressourcen an Zeit und Geld. | ||
*# Im Normalfall existieren immer widersprüchliche Anforderungen. | *# Im Normalfall existieren immer widersprüchliche Anforderungen. | ||
* Als [http://de.wikipedia.org/wiki/Optimum Optimum] bezeichnet man die beste, unter diesen Bedingungen erreichbare Lösung im Sinne eines Kompromisses zwischen verschiedenen Eigenschaften. | * Als [http://de.wikipedia.org/wiki/Optimum Optimum] bezeichnet man deshalb die beste, unter diesen Bedingungen erreichbare Lösung im Sinne eines Kompromisses zwischen verschiedenen Eigenschaften. | ||
Bei der Aufgabenstellung in einem Entwurfsprozesses handelt es sich meist nicht nur um eine "Aufgabe", sondern um ein [http://de.wikipedia.org/wiki/Problem Problem], weil ihre Lösung mit Schwierigkeiten verbunden ist und das Erreichen einer befriedigenden Lösung nicht gesichert ist: | Bei der Aufgabenstellung in einem Entwurfsprozesses handelt es sich meist nicht nur um eine "Aufgabe", sondern um ein [http://de.wikipedia.org/wiki/Problem Problem], weil ihre Lösung mit Schwierigkeiten verbunden ist und das Erreichen einer befriedigenden Lösung nicht gesichert ist: | ||
| Zeile 23: | Zeile 23: | ||
Die Anwendung von Verfahren der numerischen Optimierung zum Finden optimaler Lösungen in Entwurfsprozessen ist eine heuristische Methode: | Die Anwendung von Verfahren der numerischen Optimierung zum Finden optimaler Lösungen in Entwurfsprozessen ist eine heuristische Methode: | ||
* Grundlage ist die strukturelle Ähnlichkeit zwischen den einzelnen Phasen des Entwurfsprozesses und dem Grundprinzip der [http://de.wikipedia.org/wiki/Optimierung_(Mathematik) Optimierung als Teilgebiet der angewandten Mathematik]. | * Grundlage ist die strukturelle Ähnlichkeit zwischen den einzelnen Phasen des Entwurfsprozesses und dem Grundprinzip der [http://de.wikipedia.org/wiki/Optimierung_(Mathematik) Optimierung als Teilgebiet der angewandten Mathematik]. | ||
* Optimierung ist die Extremwertsuche (Minima bzw. Maxima) mit Randbedingungen auf einer Zielfunktion ''f'', welche die ''Güte'' eine Lösung in Abhängigkeit von den veränderlichen Variablen der Optimierungsaufgabe berechnet: | * Optimierung ist die Extremwertsuche (Minima bzw. Maxima) mit Randbedingungen auf einer Zielfunktion '''''f''''', welche die ''Güte'' eine Lösung in Abhängigkeit von den veränderlichen Variablen der Optimierungsaufgabe berechnet: | ||
<div align="center">''' Gütewert = ''f'' (Optimierungsvariablen) '''</div> | <div align="center">''' Gütewert = ''f'' (Optimierungsvariablen) '''</div> | ||
* Bei der numerischen Optimierung mit Hilfe von Computern wird meist eine Minimum-Suche betrieben. Das hat historische Gründe. Als die Computer noch mit Genauigkeiten von nur 5-6 Dezimalstellen rechneten, war dies notwendig, um kleine Absolutwert-Änderungen des Gütewertes erfassen zu können. | * Bei der numerischen Optimierung mit Hilfe von Computern wird meist eine Minimum-Suche betrieben. Das hat historische Gründe. Als die Computer noch mit Genauigkeiten von nur 5-6 Dezimalstellen rechneten, war dies notwendig, um kleine Absolutwert-Änderungen des Gütewertes erfassen zu können. | ||
* | * Bei der im Folgenden vorausgesetzten Minimum-Suche kann man sich den Gütewert als '''Distanz zur "unbekannten!" Ideallösung''' vorstellen. Die Zielfunktion muss dafür so formuliert werden, dass der Gütewert um so kleiner wird, je näher man dieser Ideallösung kommt: | ||
<div align="center">''' Zielfunktion ''f'' = numerisches Modell der Lösung + Bewertungsfunktion '''</div> | <div align="center">''' Zielfunktion ''f'' = numerisches Modell der Lösung + Bewertungsfunktion '''</div> | ||
* Die Bewertungsfunktion quantifiziert das qualitative Verhalten der aktuellen Lösung und berechnet den Gütewert (bzw. mehrere Teilgüten). | * Die zusätzlich zum Objekt-Modell der Lösung erforderliche Bewertungsfunktion quantifiziert das qualitative Verhalten der aktuellen Lösung und berechnet den Gütewert (bzw. mehrere Teilgüten). | ||
| Zeile 50: | Zeile 50: | ||
<div align="center"> '''Zielfunktion = Gütefunktion | Straffunktion''' </div> | <div align="center"> '''Zielfunktion = Gütefunktion | Straffunktion''' </div> | ||
* Der Wert der Straffunktion widerspiegelt den aktuellen Grad der Restriktionsverletzung. | * Der Wert der Straffunktion widerspiegelt den aktuellen Grad der Restriktionsverletzung. | ||
* Als Zielfunktion wird die Straffunktion benutzt, solange Restriktionen verletzt werden. Die Optimierung (Minimumsuche) führt zu Lösungen, welche keine Restriktionen mehr verletzen. | * Als Zielfunktion wird die Straffunktion benutzt, solange Restriktionen verletzt werden. Die Optimierung (Minimumsuche) auf der Straffunktion führt zu Lösungen, welche keine Restriktionen mehr verletzen. | ||
* Ist der Wert der Straffunktion=0 (d.h., es werden keine Restriktionen verletzt), so wird die Zielfunktion aus den Gütekriterien gebildet. Die Optimierung (Minimierung) führt dann zu Lösungen, welche die Wünsche möglichst gut erfüllen. | * Ist der Wert der Straffunktion=0 (d.h., es werden keine Restriktionen verletzt), so wird die Zielfunktion aus den Gütekriterien gebildet. Die Optimierung (Minimierung) auf der Gütefunktion führt dann zu Lösungen, welche die Wünsche möglichst gut erfüllen. | ||
Die Restriktionen resultieren aus den Forderungen der Aufgabenstellung, den Eigenschaften von | Die Restriktionen resultieren aus den Forderungen der Aufgabenstellung, den Eigenschaften von Lösungskomponenten und den Naturgesetzen. Deshalb unterscheidet man: | ||
# '''Funktionsbezogene Restriktionen''' - Die angestrebte Funktion wird nicht erfüllt (z.B. Prägen des Papiers, zu lange Zykluszeit). | # '''Funktionsbezogene Restriktionen''' - Die angestrebte Funktion wird nicht erfüllt (z.B. Prägen des Papiers, zu lange Zykluszeit). | ||
# '''Innere Restriktionen''' - Es werden Grenzwerte von Komponenten des modellierten Systems überschritten (Belastung der Materialien, von Bauteilen). | # '''Innere Restriktionen''' - Es werden Grenzwerte von Komponenten des modellierten Systems überschritten (z.B. Belastung der Materialien, von Bauteilen). | ||
# '''Äußere Restriktionen''' - Es werden Grenzwerte für die Umgebung des modellierten Systems überschritten (Maße, Masse, Belastung von Umgebungskomponenten mit Strom, Temperatur). | # '''Äußere Restriktionen''' - Es werden Grenzwerte für die Umgebung des modellierten Systems überschritten (z.B. Maße, Masse, Belastung von Umgebungskomponenten mit Strom, Temperatur). | ||
# '''Naturgesetzliche Restriktionen''' - Es gibt keine physikalische Entsprechung für ermittelte Kennwerte (z.B. negative Massen, Durchdringung starrer Körpern, negative Drahtlänge mit negativem ohmschen Widerstand, negative Windungszahlen). | # '''Naturgesetzliche Restriktionen''' - Es gibt keine physikalische Entsprechung für ermittelte Kennwerte (z.B. negative Massen, Durchdringung starrer Körpern, negative Drahtlänge mit negativem ohmschen Widerstand, negative Windungszahlen). | ||
| Zeile 66: | Zeile 66: | ||
Restriktionsverletzungen erscheinen als "verbotene" Bereiche mit einem Straffunktionswert>0 auf der Oberfläche der Gütefunktion. | Restriktionsverletzungen erscheinen als "verbotene" Bereiche mit einem Straffunktionswert>0 auf der Oberfläche der Gütefunktion. | ||
==== Entwurfsparameter als Teilmenge der Entwurfsgroeszen ==== | ==== Entwurfsparameter als Teilmenge der Entwurfsgroeszen ==== | ||
| Zeile 90: | Zeile 89: | ||
Nach Transformation eines Entwurfsproblems in eine Optimierungsaufgabe kann man numerische Verfahren zur (teil-)automatisierten Lösungssuche nutzen: | Nach Transformation eines Entwurfsproblems in eine Optimierungsaufgabe kann man numerische Verfahren zur (teil-)automatisierten Lösungssuche nutzen: | ||
* Es existiert eine ungeheure Vielfalt von Verfahren zur numerischen Optimierung. | * Es existiert eine ungeheure Vielfalt von Verfahren zur numerischen Optimierung. | ||
* Davon kommen für Probleme der Optimierung nichtlinearer Systeme praktisch nur Verfahren in Frage, welche die Zielfunktion (Modell+Bewertung) als Black-Box behandeln können. | * Davon kommen für Probleme der Optimierung [http://de.wikipedia.org/wiki/Nichtlineares_System nichtlinearer Systeme] praktisch nur Verfahren in Frage, welche die Zielfunktion (Modell+Bewertung) als Black-Box behandeln können. | ||
* Die unterschiedlichen Optimierungsverfahren nutzen dabei unterschiedliche Strategien, um durch methodische Variation der Entwurfsparameter das (globale) Optimum zu finden. | * Die unterschiedlichen Optimierungsverfahren nutzen dabei unterschiedliche Strategien, um durch methodische Variation der Entwurfsparameter das (globale) Optimum zu finden. | ||
* Es erfolgen Abtastschritte auf der Gütefunktion (jeweils 1 Simulationslauf mit einem bestimmten Satz der Entwurfsparameter). Damit gewinnt das jeweilige Optimierungsverfahren Informationen über die Eigenschaften der Oberfläche der Zielfunktion. | * Es erfolgen Abtastschritte auf der Gütefunktion (jeweils 1 Simulationslauf mit einem bestimmten Satz der Entwurfsparameter). Damit gewinnt das jeweilige Optimierungsverfahren Informationen über die Eigenschaften der Oberfläche der Zielfunktion. | ||
===== Hierarchische Optimierung ===== | |||
Das Programm OptiY nutzt die vom Nutzer formulierten Gütekriterien und Restriktionen als Bestandteil einer "hierarchischen" Zielfunktion: | Das Programm OptiY nutzt die vom Nutzer formulierten Gütekriterien und Restriktionen als Bestandteil einer "hierarchischen" Zielfunktion: | ||
| Zeile 112: | Zeile 111: | ||
*# Suche einer Lösungen, welche zusätzlich noch möglichst gut die Wünsche erfüllt. | *# Suche einer Lösungen, welche zusätzlich noch möglichst gut die Wünsche erfüllt. | ||
===== Straf-Funktion zur Suche zulaessiger Loesungen ===== | |||
Restriktionsverletzungen werden nach folgendem Prinzip mit "Strafpunkten" bestraft: | Restriktionsverletzungen werden nach folgendem Prinzip mit "Strafpunkten" bestraft: | ||
| Zeile 128: | Zeile 127: | ||
* Die normierte Distanz repräsentiert die Stärke der zugehörigen Restriktionsverletzung und kann als Maß für die "Bestrafung" des Modellverhaltens dienen. | * Die normierte Distanz repräsentiert die Stärke der zugehörigen Restriktionsverletzung und kann als Maß für die "Bestrafung" des Modellverhaltens dienen. | ||
* Ein quadratischer Ansatz für die Berechnung der Strafpunkte aus der normierten Distanz wichtet den Grad der Restriktionsverletzung: | * Ein quadratischer Ansatz für die Berechnung der Strafpunkte aus der normierten Distanz wichtet den Grad der Restriktionsverletzung: | ||
<div align="center"> '''''Strafpunkte = Wichtung | <div align="center"> '''''Strafpunkte = Wichtung · NormDistanz<sup>2</sup>''''' </div> | ||
[[Datei:Grundlagen_Optimierung_Strafe_nach_Normdistanz.gif|.]] | :::[[Datei:Grundlagen_Optimierung_Strafe_nach_Normdistanz.gif|.]] | ||
* Der Wert der Straf-Funktion ergibt sich als Summe aller Strafpunkte. | * Der Wert der Straf-Funktion ergibt sich als Summe aller Strafpunkte. | ||
===== Guete-Funktion zur bestmoeglichen Wunscherfuellung ===== | |||
* In OptiY wird nach jedem Simulationslauf der Wert der Straf-Funktion berechnet: | * In OptiY wird nach jedem Simulationslauf der Wert der Straf-Funktion berechnet: | ||
| Zeile 145: | Zeile 144: | ||
** Die Konvergenz zur optimalen Lösung wird in diesem Fall für nicht-evolutionäre Verfahren "zuverlässig" verhindert. | ** Die Konvergenz zur optimalen Lösung wird in diesem Fall für nicht-evolutionäre Verfahren "zuverlässig" verhindert. | ||
===== Mehrkriterien-Optimierung ===== | |||
In der Produktentwicklung enthalten die bei der Aufgabenpräzisierung erarbeiteten Anforderungslisten im Normalfall unterschiedlichste Wünsche, welche mit unterschiedlichen Prioritäten möglichst gut zu erfüllen sind: | |||
<div align="center"> | * Die aus den Entwurfsproblemen abgeleiteten Optimierungsaufgaben besitzen dann nicht nur ein Gütekriterium, sondern mehrere Teilgüten. Die Werte aller dieser Teilgüten sollen bei der Optimierung möglichst weit minimiert werden. | ||
* Bei der klassischen monokriteriellen Optimierung wird die erforderliche Zielfunktion als Summe der gewichteten Teilgüten gebildet, wobei die Wichtungsfaktoren die Prioritäten der Wünsche widerspiegeln: | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Gesamtguete_mit_Wichtung.gif|.]] </div> | |||
Leider sind die Teilgüten meist nicht miteinander verträglich. Beim Versuch, die Werte einiger Teilgüten zu minimieren, können sich die Werte anderer Kriterien vergrößern (z.B. "geringe Ungenauigkeit" widerspricht bei einem Messgerät meist "geringen Kosten"). Deshalb ist Vorgabe von Gewichtungsfaktoren meist eine sehr grobe Vereinfachung, denn es gibt keine eindeutige Lösung, sondern eine pareto-optimale Lösungsmenge: | |||
* | * Zur Veranschaulichung dieser Lösungsmenge wird der Lösungsraum für die Entwurfsvarianten über die (normierten) Teilgüten aufgespannt (jeder Teilgüte ist eine Koordinaten-Achse zugeordnet): | ||
** | <div align="center"> [[Datei:Software_SimX_-_Nadelantrieb_-_Robust-Optimierung_-_paretomenge.gif|.]] </div> | ||
* Die Varianten der Pareto-Menge sind "besser" als die übrigen Varianten. | |||
* Letztendlich entscheiden die Verwertungsbedingungen darüber, was man als optimale Kompromisslösung wählt, z.B.: | |||
*# möglichst schnell, egal wie teuer | |||
*# möglichst billig, egal wie schnell | |||
*# möglichst gutes Preis/Leistungsverhältnis (solides Produkt zum angemessenen Preis) | |||
Aktuelle Version vom 6. Februar 2014, 13:11 Uhr
Transformation von Entwurfsproblemen in Optimierungsaufgaben
Ideale und reale Loesungen
Im Rahmen eines Entwurfsprozesses wird für eine gegebene Aufgabenstellung die "ideale Lösung" gesucht:
- Die ideale Lösung soll alle Forderungen und Wünsche der präzisierten Aufgabenstellung perfekt erfüllen.
- Im allgemeinen ist die technische Realisierung der anzustrebenden Lösung zu Beginn des Entwurfsprozesses unbekannt:
- Leider muss man sich am Ende des Entwurfsprozesses mit einer Kompromiss-Lösung zufrieden geben:
- Man verfügt nur über begrenzte Ressourcen an Zeit und Geld.
- Im Normalfall existieren immer widersprüchliche Anforderungen.
- Als Optimum bezeichnet man deshalb die beste, unter diesen Bedingungen erreichbare Lösung im Sinne eines Kompromisses zwischen verschiedenen Eigenschaften.
Bei der Aufgabenstellung in einem Entwurfsprozesses handelt es sich meist nicht nur um eine "Aufgabe", sondern um ein Problem, weil ihre Lösung mit Schwierigkeiten verbunden ist und das Erreichen einer befriedigenden Lösung nicht gesichert ist:
- Der Bearbeiter muss bei der Problemlösung heuristisch vorgehen, da für den Entwurfsprozess keine Algorithmen existieren, welche das Erreichen einer Lösung garantieren.
- Heuristik ist ein erkenntnistheoretisches Verfahren mit dem Zweck, durch Entwicklung und Anwendung von meist unbewiesenen Methoden neue Erkenntnisse zu gewinnen (Erfindungskunst, von griechisch heuriskein = finden):
- Heuristische Methoden basieren auf Erfahrungen.
- Sie können auch auf falschen Erfahrungen (z.B. Scheinkorrelationen) basieren und trotzdem zu brauchbaren Lösungen führen.
Numerische Optimierung als heuristische Methode
Die Anwendung von Verfahren der numerischen Optimierung zum Finden optimaler Lösungen in Entwurfsprozessen ist eine heuristische Methode:
- Grundlage ist die strukturelle Ähnlichkeit zwischen den einzelnen Phasen des Entwurfsprozesses und dem Grundprinzip der Optimierung als Teilgebiet der angewandten Mathematik.
- Optimierung ist die Extremwertsuche (Minima bzw. Maxima) mit Randbedingungen auf einer Zielfunktion f, welche die Güte eine Lösung in Abhängigkeit von den veränderlichen Variablen der Optimierungsaufgabe berechnet:
- Bei der numerischen Optimierung mit Hilfe von Computern wird meist eine Minimum-Suche betrieben. Das hat historische Gründe. Als die Computer noch mit Genauigkeiten von nur 5-6 Dezimalstellen rechneten, war dies notwendig, um kleine Absolutwert-Änderungen des Gütewertes erfassen zu können.
- Bei der im Folgenden vorausgesetzten Minimum-Suche kann man sich den Gütewert als Distanz zur "unbekannten!" Ideallösung vorstellen. Die Zielfunktion muss dafür so formuliert werden, dass der Gütewert um so kleiner wird, je näher man dieser Ideallösung kommt:
- Die zusätzlich zum Objekt-Modell der Lösung erforderliche Bewertungsfunktion quantifiziert das qualitative Verhalten der aktuellen Lösung und berechnet den Gütewert (bzw. mehrere Teilgüten).
Wuensche als Guetekriterien
- Wie in den Grundlagen zum Entwurfsprozess beschrieben, sollte ein Entwurfsproblem während der Aufgabenpräzisierung in Form einer Anforderungsliste beschrieben werden:
- Wünsche:
- Qualitative Anforderungen im Sinne "möglichst ...." (schnell, billig, leise usw.)
- Forderungen:
- Quantitative Anforderungen, die unbedingt zu erfüllen sind
(z.B. Verlustleistung < 1 W, Geschwindigkeit > 1 m/s, Temperatur zwischen 20°C und 100°C)
- Quantitative Anforderungen, die unbedingt zu erfüllen sind
- Damit ein Optimierungstool auf die "Wünsche" und "Forderungen" der Aufgabenstellung Bezug nehmen kann, müssen diese durch entsprechende Modellgrößen (Parameter / Variablen) repräsentiert werden.
- Dabei sollte der Erfüllungsgrad eines Wunsches wertemäßig als Distanz zur "idealen" Wunscherfüllung im Modell abgebildet werden.
- Nutzt man die zugehörige Variable in einem Optimierungstool als Gütekriterium, so führt die Minimierung des Wertes zu einer Annäherung an die gewünschte ideale Lösung.
Forderungen als Restriktionen
Die Verfahren der numerischen Optimierung gestatten die Berücksichtigung von Randbedingungen (Restriktionen), indem bei Restriktionsverletzungen eine Straffunktion mit einem Wert>0 gebildet wird:
- Der Wert der Straffunktion widerspiegelt den aktuellen Grad der Restriktionsverletzung.
- Als Zielfunktion wird die Straffunktion benutzt, solange Restriktionen verletzt werden. Die Optimierung (Minimumsuche) auf der Straffunktion führt zu Lösungen, welche keine Restriktionen mehr verletzen.
- Ist der Wert der Straffunktion=0 (d.h., es werden keine Restriktionen verletzt), so wird die Zielfunktion aus den Gütekriterien gebildet. Die Optimierung (Minimierung) auf der Gütefunktion führt dann zu Lösungen, welche die Wünsche möglichst gut erfüllen.
Die Restriktionen resultieren aus den Forderungen der Aufgabenstellung, den Eigenschaften von Lösungskomponenten und den Naturgesetzen. Deshalb unterscheidet man:
- Funktionsbezogene Restriktionen - Die angestrebte Funktion wird nicht erfüllt (z.B. Prägen des Papiers, zu lange Zykluszeit).
- Innere Restriktionen - Es werden Grenzwerte von Komponenten des modellierten Systems überschritten (z.B. Belastung der Materialien, von Bauteilen).
- Äußere Restriktionen - Es werden Grenzwerte für die Umgebung des modellierten Systems überschritten (z.B. Maße, Masse, Belastung von Umgebungskomponenten mit Strom, Temperatur).
- Naturgesetzliche Restriktionen - Es gibt keine physikalische Entsprechung für ermittelte Kennwerte (z.B. negative Massen, Durchdringung starrer Körpern, negative Drahtlänge mit negativem ohmschen Widerstand, negative Windungszahlen).
Werden Restriktionen nicht direkt durch Modellgrößen (Parameter, Ergebnisse) im Objektmodell repräsentiert, müssen zusätzlich im Modell entsprechende Bewertungsgrößen (Ergebnisse) definiert und berechnet werden (z.B. Prägung, Zykluszeit, Maximum des Spulenstroms usw.).
- Restriktionsverletzungen = unzulässige Lösungen:
- Restriktionsgrößen liegen außerhalb ihres zulässigen Wertebereiches oder
- Entwurfsparameter liegen außerhalb ihrer zulässigen Grenzen (außerhalb des Suchraums)
Restriktionsverletzungen erscheinen als "verbotene" Bereiche mit einem Straffunktionswert>0 auf der Oberfläche der Gütefunktion.
Entwurfsparameter als Teilmenge der Entwurfsgroeszen
- Entwurfsgrößen:
- sind geometrisch-stoffliche Kenngrößen des zu konstruierenden Objekts, die man in der jeweiligen Entwurfsetappe ermitteln (bzw. präzisieren) möchte. Meist treten Sie als Parameter im Modell auf.
- Entwurfsparameter (als Teilmenge der Entwurfsgrößen):
- sind diejenigen Modellparameter, welche während des Optimierungsexperiments vom gewählten Optimierungsverfahren automatisch variiert werden, um eine optimale Lösung zu finden. Man nennt sie auch Optimierungsvariable:
- Die Entwurfsparameter definieren die Größe des Suchraums bei der Suche nach der optimalen Lösung.
- Für die ausgewählten Entwurfsparameter ist jeweils ein zulässiger Variationsbereich zu definieren. Ein Verlassen des zulässigen Bereiches wird wie eine Restriktionsverletzung gewertet.
- Vor Durchführung eines Optimierungsexperiments sind (meist) umfangreiche Vorüberlegungen zur Wahl der Entwurfsparameter und ihrer zulässigen Variationsbereiche erforderlich.
- sind diejenigen Modellparameter, welche während des Optimierungsexperiments vom gewählten Optimierungsverfahren automatisch variiert werden, um eine optimale Lösung zu finden. Man nennt sie auch Optimierungsvariable:
Um den Suchraum möglichst klein zu halten, sollte man möglichst wenige Entwurfsparameter mit möglichst kleinem Variationsbereich verwenden:
- Welche Stoff-/Geometrieparameter können vorläufig als Festwerte betrachtet werden (z.B. Vorgaben aus der Aufgabenstellung)?
- Welche Parameter darf man nicht unabhängig voneinander verändern? Diese sollten über ihre Abhängigkeiten miteinander verknüpft werden (z.B. geometrische Passfähigkeiten).
- Durchführung von Einflussanalysen, um ein Gefühl dafür zu entwickeln, welche Wirkung die Veränderung der freien Parameter und Anfangswerte auf das Modellverhalten hat. Dabei gewinnt man auch Erkenntnisse zu sinnvollen Variationsbereichen für die einzelnen Parameter.
- Für die noch zu ermittelnden Entwurfsgrößen sollte man eine Rangfolge anhand ihres Einflusses auf das gewünschte Verhalten definieren. Nach einer Groboptimierung der einflussreichsten Entwurfsgrößen können in einer anschließenden Feinoptimierung auch die weniger einflussreichen Entwurfsgrößen mit einbezogen werden.
Loesungssuche mit Optimierungsverfahren
Nach Transformation eines Entwurfsproblems in eine Optimierungsaufgabe kann man numerische Verfahren zur (teil-)automatisierten Lösungssuche nutzen:
- Es existiert eine ungeheure Vielfalt von Verfahren zur numerischen Optimierung.
- Davon kommen für Probleme der Optimierung nichtlinearer Systeme praktisch nur Verfahren in Frage, welche die Zielfunktion (Modell+Bewertung) als Black-Box behandeln können.
- Die unterschiedlichen Optimierungsverfahren nutzen dabei unterschiedliche Strategien, um durch methodische Variation der Entwurfsparameter das (globale) Optimum zu finden.
- Es erfolgen Abtastschritte auf der Gütefunktion (jeweils 1 Simulationslauf mit einem bestimmten Satz der Entwurfsparameter). Damit gewinnt das jeweilige Optimierungsverfahren Informationen über die Eigenschaften der Oberfläche der Zielfunktion.
Hierarchische Optimierung
Das Programm OptiY nutzt die vom Nutzer formulierten Gütekriterien und Restriktionen als Bestandteil einer "hierarchischen" Zielfunktion:
- Um zwei Lösungen miteinander vergleichen zu können, muss für jede dieser Lösungen ein Zielfunktionswert nach der gleichen Zielfunktion gebildet werden. Der Zielfunktionswert entspricht der "Güte" oder "Fitness" einer Lösung.
- OptiY benutzt dafür drei verschiedene Zielfunktionen
- Straf-Funktion für die Begrenzung des Suchraums (interne "unsichtbare" Größe)
- Straf-Funktion für Restriktionsverletzungen (auf Basis der vom Nutzer definierten Forderungen)
- Güte-Kriterien für zulässige Lösungen (vom Nutzer definierte Wünsche)
- Die 1. Zielfunktion hat eine höhere Priorität als die 2. Zielfunktion. Diese hat eine höhere Priorität als die 3. Zielfunktion.
- Für den Vergleich der Fitness zweier Lösungen wird die Zielfunktion mit der höchsten Priorität benutzt:
- Liegt mindestens eine Lösung außerhalb des durch die Grenzen der Optimierungsvariablen aufgespannten Suchraums, so wird die 1. Zielfunktion benutzt.
- Gibt es bei mindestens einer Lösung noch Restriktionsverletzungen, so wird die 2. Zielfunktion benutzt.
- Nur wenn beide Lösungen im zulässigen Bereich liegen, werden die Gütekriterien für die Bewertung benutzt.
- Die hierarchische Optimierung entspricht der Vorgehensweise bei der Erarbeitung einer optimalen Lösung für eine Entwurfsaufgabe:
- Ausblenden von Lösungen, welche außerhalb des zulässigen Bereiches für die Entwurfsparameter liegen.
- Suche einer Lösungen, welche alle Forderungen erfüllt.
- Suche einer Lösungen, welche zusätzlich noch möglichst gut die Wünsche erfüllt.
Straf-Funktion zur Suche zulaessiger Loesungen
Restriktionsverletzungen werden nach folgendem Prinzip mit "Strafpunkten" bestraft:
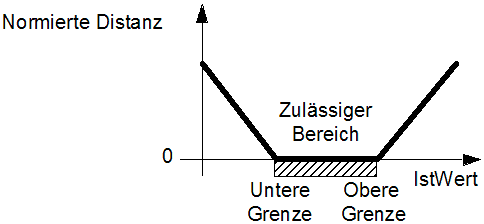
- Für jede Restriktionsgröße wird die Distanz zum zulässigen Wertebereich berechnet (UG=untere Grenze / OG=obere Grenze):
Distanz = 0 : wenn UG ≤ Istwert ≤ OG) Distanz = abs (IstWert-OG) : wenn IstWert > OG Distanz = abs (IstWert-UG) : wenn IstWert < UG
- Es erfolgt eine Normierung der Distanz auf die Bereichsbreite:
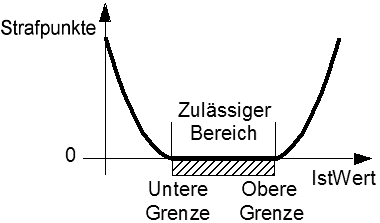
- Die normierte Distanz repräsentiert die Stärke der zugehörigen Restriktionsverletzung und kann als Maß für die "Bestrafung" des Modellverhaltens dienen.
- Ein quadratischer Ansatz für die Berechnung der Strafpunkte aus der normierten Distanz wichtet den Grad der Restriktionsverletzung:
- Der Wert der Straf-Funktion ergibt sich als Summe aller Strafpunkte.
Guete-Funktion zur bestmoeglichen Wunscherfuellung
- In OptiY wird nach jedem Simulationslauf der Wert der Straf-Funktion berechnet:
- Eine zulässige Lösung im Sinne der Forderungen (Restriktionen) liegt vor, wenn der Wert der Straf-Funktion = 0 ist.
- Die Suche eines zulässigen Lösungsbereiches besitzt bei der hierarchischen Optimierung höchste Priorität.
- Erst im Bereich der zulässigen Lösungen werden für die Optimum-Suche die Gütekriterien (Wünsche) berücksichtigt:
- Damit existieren für das Optimierungsverfahren innerhalb des Suchraumes zwei Zielfunktionen (Straf-Funktion und Güte-Funktion).
- Die Umschaltung zwischen beiden Zielfunktionen erfolgt beim Übergang zwischen Bereichen unzulässigen und unzulässigen Lösungen.
- Probleme durch Umschaltung der Zielfunktionen:
- Eine bessere Erfüllung von Wünschen führt bei technischen Problemstellungen meist wieder zu Restriktionsverletzungen.
- Damit schaltet der Optimierungsprozess an der Grenze ständig zwischen den zwei Zielfunktionen hin und her (Konflikt zwischen Wunsch- und Pflichterfüllung).
- Die Konvergenz zur optimalen Lösung wird in diesem Fall für nicht-evolutionäre Verfahren "zuverlässig" verhindert.
Mehrkriterien-Optimierung
In der Produktentwicklung enthalten die bei der Aufgabenpräzisierung erarbeiteten Anforderungslisten im Normalfall unterschiedlichste Wünsche, welche mit unterschiedlichen Prioritäten möglichst gut zu erfüllen sind:
- Die aus den Entwurfsproblemen abgeleiteten Optimierungsaufgaben besitzen dann nicht nur ein Gütekriterium, sondern mehrere Teilgüten. Die Werte aller dieser Teilgüten sollen bei der Optimierung möglichst weit minimiert werden.
- Bei der klassischen monokriteriellen Optimierung wird die erforderliche Zielfunktion als Summe der gewichteten Teilgüten gebildet, wobei die Wichtungsfaktoren die Prioritäten der Wünsche widerspiegeln:
Leider sind die Teilgüten meist nicht miteinander verträglich. Beim Versuch, die Werte einiger Teilgüten zu minimieren, können sich die Werte anderer Kriterien vergrößern (z.B. "geringe Ungenauigkeit" widerspricht bei einem Messgerät meist "geringen Kosten"). Deshalb ist Vorgabe von Gewichtungsfaktoren meist eine sehr grobe Vereinfachung, denn es gibt keine eindeutige Lösung, sondern eine pareto-optimale Lösungsmenge:
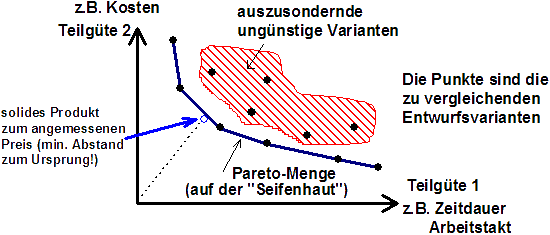
- Zur Veranschaulichung dieser Lösungsmenge wird der Lösungsraum für die Entwurfsvarianten über die (normierten) Teilgüten aufgespannt (jeder Teilgüte ist eine Koordinaten-Achse zugeordnet):
- Die Varianten der Pareto-Menge sind "besser" als die übrigen Varianten.
- Letztendlich entscheiden die Verwertungsbedingungen darüber, was man als optimale Kompromisslösung wählt, z.B.:
- möglichst schnell, egal wie teuer
- möglichst billig, egal wie schnell
- möglichst gutes Preis/Leistungsverhältnis (solides Produkt zum angemessenen Preis)